• Use an exit ticket (M-2-5-2_Exit Ticket Lesson 2 and KEY.docx) to assess student understanding of partitioning shapes into equal parts. Make a copy of the exit ticket for each student. Hand out the tickets at the end of the lesson and collect them as students walk out the door.
• Listen to and observe students as they work to partition shapes into equal parts.

This lesson begins with students discussing how to share a cookie with one other person, partitioning the cookie into halves so each person gets the same amount. The lesson continues with an exploration of folding and cutting shapes to partition the shapes into halves, thirds, and fourths. The folding and cutting activities are intended to help students understand that all parts must be equal in size when naming fractions. Students who need opportunities for additional practice with these activities will be able to fold familiar shapes into halves at a workstation.

Say, “Have you ever had a cookie that you had to share with someone else, such as a brother, sister, cousin, or friend? How did you split the cookie to be sure both of you got the same amount?”

Distribute a paper circle 4” in diameter to each student; or use the Partitioning Circles sheet (M-2-5-2_Partitioning Circles.docx). Hold up a paper circle. Tell students to pretend it is a delicious chocolate chip cookie. Ask two students to come to the front of the class. Ask, “How could we cut the cookie so both you and your friend get the same amount?” Ask students to volunteer their suggestions by drawing their proposed cut lines on their cookies. Now say, “Using scissors, decide if cutting the cookie on this line results in both people getting the same amount of the cookie.” Let students cut on this line and determine that both people would get the same amount of cookie if each resulting piece is the same size. Many students will eventually think about putting the one piece on top of the other to check their relative sizes. After students seem to be finished cutting and checking the sizes of their pieces, ask, “When you cut on the line you drew, did both people get the same amount of cookie? How did you decide if each person got the same amount?” Allow students to explain how they checked the relative sizes of the pieces.

Distribute another paper circle 4” in diameter to each student. Hold the paper circle up and explain that this is again the cookie. “If this was a cookie, fold the cookie so both you and your friend get the same amount.” After students seem to be finished folding, ask, “When you folded your cookie, did both people get the same amount of cookie? How did you decide if each person got the same amount?” Some students may suggest folding the paper cookie in half and creasing it to find the proper fold line. Introduce the terms half or halves. Explain to students that each of the two equal parts is called one half of the cookie, and the two halves of a cookie make the whole cookie.

Have students tape or glue their cookie divided into halves into their math journals. Ask them to write the word half and the fraction 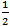 in each of the two equal sections of the circle, and write
2 halves = 1 whole below the circle.

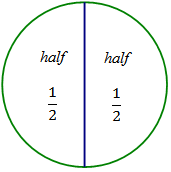
2 halves = 1 whole

Distribute a paper circle 4” in diameter to each student. Hold a paper circle up. Ask four students to come up to the front of the class. Ask, “If this was a cookie, how could you cut the cookie so these four friends each get the same amount?” Ask students to try to fold the circle to partition it into four equal parts. When students appear to be finished with the folding, ask, “How did you fold your cookie so you have four equal parts? How are you sure each part is equal in size?”

As students are working, walk around and assess their work. After students complete their folding, have them cut along the lines to be sure all parts are equal in size. Students should tape or glue their circles, divided into fourths, into their math journals. Ask them to write the word fourth and the fraction 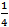 in each of the four equal sections of the circle, and write 4 fourths = 1 whole below the picture.

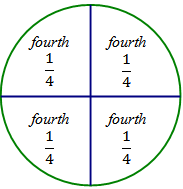
4 fourths = 1 whole

Distribute a paper circle 4” in diameter to each student. Hold a paper circle up. Ask students, “If this was a cookie, how could you cut the cookie so both you and two of your friends, a total of three people, each got the same amount?” Ask students to try to fold or cut the circle to partition it into three equal parts. When students have had the opportunity to realize the difficulty of this task, ask, “Were you able to fold or cut your cookie so you have three equal parts?” Explain that dividing shapes into three equal parts is often more difficult than dividing into two or four equal parts.

Give each student a paper circle 4” in diameter that has cut lines indicating thirds of the circle (M-2-5-2_Partitioning Circles into Thirds.docx). Ask students to use scissors to verify that these cut lines do indeed partition the cookie into three equal parts.

After students have finished cutting the thirds, students should tape or glue their circles into their math journals. Ask them to write the word third and the fraction 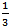 in each of the three equal sections of the circle, and write 3 thirds = 1 whole below the picture.

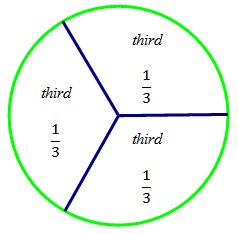
3 thirds = 1 whole

Distribute three copies of each shape (triangles, squares, and rectangles) from the Partitioning Shapes sheet (M-2-5-2_Partitioning Shapes.docx) to each student (a total of nine shapes per student). Ask students to partition each shape into halves, thirds, and fourths. Students should also tape or glue these shapes into their math journals. Partitioning the shapes into thirds will be the most challenging for students. You may have to work together as a class to partition some shapes into thirds.

Extension:

Use the activities and strategies listed below to meet the needs of your students during the year.

• Routine: Use any opportunity that naturally arises in the classroom to review unit fractions, including halves, thirds, and fourths. For example, if half of the class gets to line up for lunch first, ask the students how to decide how many students are in half the class. Also, partition sets of objects and shapes into halves, thirds, and fourths when the opportunities arise.
• Expansion: Students who are ready can try partitioning other shapes into halves, thirds, and fourths. A trapezoid, pentagon, hexagon, and octagon are available for students to cut out in the Expansion resource (M-2-5-2_Expansion.docx).
• Small Groups: Prepare a workstation to explore and review ways to partition shapes into halves. At the workstation, have paper shapes including squares, equilateral triangles, isosceles triangles, rectangles, pentagons, and hexagons that students can fold in half. Provide both regular and irregular shapes labeled with numbers to give students experiences with symmetrical and asymmetrical figures. Students should be encouraged to fold the shapes in different ways to investigate if there are multiple ways to fold the shape in half. Ask students to fold these same shapes into fourths. Have them make a list by number of the shapes they could and could not fold into halves. Have them use crayons to color their fold lines. Students can share their work with the class.