• Use the random reporter strategy for student observations in the introduction activity to obtain an understanding of students’ comfort level with concepts. [IS.7 - All Students]
  

• Observations during the Recording Rotations Activity will allow for clarifications and corrections as needed.

• The evaluation of the Initials Rotation Project should help to determine which students are ready to work beyond the standards and which students may benefit from additional instruction.

• Use the Lesson 2 Exit Ticket (M-5-7-2_Lesson 2 Exit Ticket.doc and M-5-7-2_Lesson 2 Exit Ticket KEY.doc) for further evaluation.

[IS.6 - All Students]

[IS.3 - Struggling Learners] Prior to class, cut out four congruent geometric figures such as parallelograms or trapezoids using colorful paper. Arrange them on the front board or wall placing the original on or centered over 0°, and the other figures rotated 90°, 180°, and 270°. An option, if the classroom is set up to project images from your computer, is to create and project a rotated design using http://www.mathsisfun.com/geometry/symmetry-artist.html.

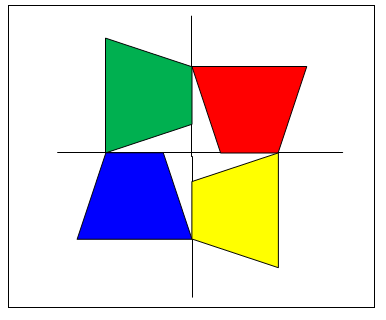
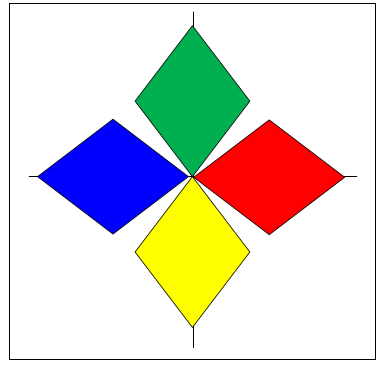
[IS.2 - All Students] Ask students to write three observations about the arrangement of the shapes on a piece of paper. Randomly select several students to share their observations. Make note of the trapezoid example where one side of the original (red) figure rests on the axis line of 0°. The remaining figures are rotated not reflected. The same side of each figure is resting against the axis lines at 90°, 180°, and 270°. Each point touching an axis is the same distance from the origin in each rotation. If the red figure is considered to be the original figure, moving counter clockwise is the 90^◦ rotation (green figure), the 180° rotation (blue figure), and the 270° rotation (yellow figure). It is also interesting to note the pattern created by the trapezoids on the inside white space by the origin.

The parallelogram pattern has each figure centered on the degree markings rather than resting on them. It may also be noted that while these figures were rotated, it also appears that they were reflected (flipped) over the horizontal axis (green to yellow) and over the vertical axis (red to blue).

“In today’s lesson we will be working with designs that are created by rotating figures. The number of degrees we rotate each figure is called the angle of rotation. Like our reflections from Lesson 1, we will be analyzing and creating designs that have symmetry. This will be a different type of symmetry known as rotational symmetry.”

“We will begin by rotating figures at your desk. Each of you will receive a piece of cardboard, two coordinate axes, a geometric figure, and a push pin. It is very important that you only push your pin into the paper when the cardboard is below it to protect your desk top.”

Hand out one piece of cardboard, [IS.5 - All Students] two Coordinate Axes sheets (M-5-7-2_Coordinate Axes.doc), one geometric shape (M-5-7-2_Push Pin Figures.doc), and a push pin to each student. Instruct students to place one sheet of the axes paper down on the cardboard. Bring tape around to help students secure the page onto the cardboard.

Note to teacher: You may want to lightly tape one axis page on the front and back of the cardboard pieces in advance to save time during the activity.

Students will use the paper models on the set of coordinate axes to observe what happens when shapes are rotated. Students will use either a rectangle or triangle cutout. The shape should be pinned down, but it should still be able to rotate about the origin.

“Now we are ready to begin. Take your geometric figure and place one corner of it at the origin (center) of your coordinate axes and one edge on top of the x-axis at 0° like I did on my trapezoid example on the board. Very carefully push your pin into that same vertex of your geometric shape as close to the origin as you can get it.” Walk around and assist students.

“Trace your shape with your pencil. Now, leaving your pin in place, rotate your figure 90°counter clockwise (to the left). Be sure to line it up in the same position as it was originally placed relative to the axis. When you are sure it is in the correct place, trace it. Raise your hand if you need assistance.” Visually confirm that each student has correctly traced the rotation. Then, repeat this process for 180°, 270°, and 360°.

“What did you notice when you rotated 360°?” (the figure overlapped exactly on the original traced figure)

“Let’s try something else. Take your pin and figure off of the cardboard and flip your cardboard over. We will be using your second Coordinate Axis sheet. This time pin the vertex of your figure to the origin (center), but with the figure centered over the x-axis at 0^◦ like my parallelogram example.” Repeat the steps done on the first side.

“The designs you just created have rotational symmetry. If a design or figure has rotational symmetry, when rotated counter clockwise on a fixed interior point, it will completely coincide (overlap) with the original at least once before it is rotated the full 360°. The number of degrees it is rotated to get to the first overlap is called the degree of rotation. What is our degree of rotation?” (90°)

“In one full turn (360°), how many times would our design be able to rotate and rest (overlap) entirely on the original design?” (4)

Demonstrate with an equilateral triangle, rotating it with a push pin in its center rather than a vertex, to help students understand the action. Make note that there are only three positions when rotated about its own center, whereas there could be four positions if rotated about the origin. Compare this to putting a push pin at the center (origin) of any of the student designs and rotating the entire design. Demonstrate this rotation movement with one of the student’s designs, or have a student demonstrate it on his/her own axes using the push pin at the center of the figure to rotate it.

Recording Rotations Activity

“With your partner you will determine whether some additional shapes have rotational symmetry and the degree of rotation for those that do.”

Hand out the Rotational Symmetry record sheet (M-5-7-2_Rotational Record.doc and M-5-7-2_Rotational Record KEY.doc) and a bag of pattern cutouts left from Lesson 1 (M-5-7-1_Pattern Cutouts 1.doc, M-5-7-1_Pattern Cutouts 2.doc), along with Pattern Cutouts 3 (M-5-7-2_Pattern Cutouts 3.doc). Allow students to use the cardboard and push pin to experiment with the cutouts. If the degree of rotation (those other than 90°, 180°, and 270°) is unknown to students, encourage students to find a way to calculate or estimate a logical value. Circulate among the groups to help clarify misconceptions. Have the teacher key available for students to check their own work or to check it for them (M-5-7-2_Rotational Record KEY.doc). When they have successfully completed the Recording Rotations activity, instruct students to begin the Initials Rotation Project. If the initials are not completed during class, this could be used as a take-home project.

Initials Rotation Project (in class or take home):

Provide each student with another Coordinate Axis page (M-5-7-2_Coordinate Axes.doc). Students will write their initials in capital letters with a symbol on each side of the initials on the x-axis at 0°. The letters should be in a creative pattern or design. The symbols can be the same as those used in the Lesson 1 Name Card activity, or they can be different. The symbols should represent something about the students or something they like such as a flower or a basketball. Instruct students to rotate their initials design 90°, 180°, and 270°. Provide markers, crayons, or colored pencils. Students should draw the outline in pencil first and add the design color once they have correctly rotated their initials. Allow students approximately 20­–30 minutes to work. If more time is needed, this project could be finished at home.

Monitor students while they work on the Recording Rotations and Initials Rotation projects. Ask students to share their ideas and findings. Have students demonstrate specific rotations and ask for their observations with their project elements. Make suggestions or use clarifying questions to guide students who have misconceptions. Encourage students to make adjustments as necessary. Within each pair or small group, ask at least one student to summarize the meaning of rotational symmetry and engage in a short discussion with the group. Assess whether students can distinguish between reflectional (mirror) and rotational symmetry.

Each student should complete the Exit Ticket at the end of the lesson (M-5-7-2_Lesson 2 Exit Ticket.doc and M-5-7-2_Lesson 2 Exit Ticket KEY.doc). Use the results to determine which, if any, additional instructional strategies suggested below are appropriate for individual students.

Extension:

Use the following suggestions to tailor this lesson to meet the needs of your students during the unit and throughout the year.

• Routine:Discuss the importance of understanding and using the correct vocabulary words to communicate mathematical ideas clearly. During this lesson, the following terms should be entered into students’ Vocabulary Journals (M-5-7-1_Vocabulary Journal.doc): angle of rotation, coordinate axes, edge, origin, rotational symmetry, and vertex. Keep a supply of Vocabulary Journal pages on hand so students can add pages as needed. Bring up instances of rotation and rotational symmetry as seen throughout the school year. Ask students to bring up examples that they see (signs, hubcaps, flowers, etc.). Have a special place in the room, such as a bulletin board, to post pictures of symmetry students have found and shared with the class. Post and label the type of symmetry and degree of rotation if it is a rotational example.

• Small Group:Rotation Practice

Extra practice is necessary for students who are having difficulty with the concept of rotation. Work directly with these students in a small group while other students work at stations or on the extension activity. Provide students with a Coordinate Axis sheet (M-5-7-2_Coordinate Axes.doc). Also provide a variety of pattern blocks or pattern cutouts (M-5-7-1_Pattern Cutouts 1.doc, M-5-7-1_Pattern Cutouts 2.doc, or M-5-7-2_Pattern Cutouts 3.doc). Begin by having students place one figure at 0°. Demonstrate a 90°rotation on a coordinate grid, and then allow students to practice with supervision and assistance. Continue practicing by rotating the individual cutout to 180°, 270°, and 360°. As students master these rotations, move to a figure created by combining two pattern blocks or cutouts. Tape the pattern pieces together to start if students are having difficulty manipulating the pieces during the rotation. Move on to more complicated designs as time permits.

• Station 1:Snowflake Symmetry

Provide square sheets of paper which are cut to 8 x 8 inches, 9 x 12 colored sheets of paper, glue sticks, and scissors. Post the directions page at the station (M-5-7-2_Snowflake Station.doc). Ask students to glue their snowflake onto a colored sheet of paper, leaving room to write below it. Direct students to write a description of the symmetry involved in their snowflake. A variation is to have students describe the symmetry verbally to you, to a small group, or to the entire class rather than write it down. Have students hang their unique creation at the station or another specified location.

• Station 2:Hubcap and Sign Symmetry

Provide a variety of magazines, scissors, glue sticks, and lined paper. Auto magazines and advertisements are good choices because of the types of pictures students are trying to find. Have students cut out 3–5 pictures of signs and/or hubcaps that have rotational symmetry or multiple forms of symmetry. If it is difficult to find enough pictures for each student, have students work in pairs. Another option is to place a different topic as a title on top of each page based on the magazines that are available (such as fashion, food, home décor, auto, company logos, sports, etc.). Ask students to cut examples out and glue them onto their paper. Below each picture, ask students to describe the symmetry incorporated in the design. If time permits, ask students to create a hubcap design or new traffic sign of their own using rotational symmetry.

• Expansion:Kaleidoscope Symmetry Project

Many wallpaper, floor covering, fabric, quilt square, and kaleidoscope designs use patterns with both reflective and rotational symmetry. Display several examples such as the ones below. Ask students to use pattern blocks or pattern cutouts to create a kaleidoscope pattern that exhibits both rotational symmetry and reflective symmetry (M-5-7-1_Pattern Cutouts 1.doc, M-5-7-1_Pattern Cutouts 2.doc, and M-5-7-2_Pattern Cutouts 3.doc). Suggest that students begin by creating one triangular pattern first (60°, 90°, or 120° central angle) and then reflecting and rotating this to complete the full design. Provide a coordinate grid (M-5-7-2_Coordinate Axes.doc) on which students can arrange the pattern blocks. You may want to assist by drawing one triangular outline on the grid paper before copies are made, so students are given the first part of the design. When the design is complete, have students trace the pieces and color the design.

Kaleidoscope examples:

Quilt square examples:

This lesson is organized to be exploratory in nature. Hands-on projects with student summaries at the end of each activity help reinforce the concepts in students’ minds and allow the instructor to evaluate understanding. The lesson began with a demonstration of rotation in which students made observations about the characteristics of rotated figures. Students were asked to rotate figures of their own in two different ways. The lesson scaffolds on the reflective symmetry explored in Lesson 1 by using similar vocabulary and similar activities, and by comparing the types of symmetry explored in both lessons. In the expansion at the end of the lesson, students are asked to combine rotational and reflective symmetry in the same design. Lesson 3 will continue to scaffold and will bring in translational transformations.