Absolute Value Functions

Objectives

In this unit, students will model absolute value functions. Students will:

create a table of values and graphs of absolute value functions.
develop an understanding of transformations of absolute value functions.
model real-world situations with absolute value functions and interpret components of the function, including vertex, domain, range, and rate of change.
develop the ability to imagine real-world scenarios best modeled by absolute value functions.

Essential Questions

How can a given function be represented? What connections can be made between the various representations?
Which function best models a given real-world scenario? What does the function look like in the real world?
How can an equation, table, and graph be used to analyze the rate of change and other applicable information, related to a real-world problem and the representative function?

Vocabulary

Absolute Value Function: A function in the form of , where a ≠ 0. [IS.1 - Preparation]
Dependent Variable: The variable representing range values of a function, commonly the y-term.
Domain: The set of x-values or input values of a function.
Independent Variable: The variable representing domain values of a function, commonly the x-term.
Range: The set of y-values or output values of a function.
Vertex: The point, or ordered pair, that represents the minimum or maximum of a function.
Rate of Change: The difference in the change in y-values per change in x-values (e.g., slope).

Duration

90–120 minutes/1–2 class periods [IS.2 - All Students]

Prerequisite Skills

Prerequisite Skills haven't been entered into the lesson plan.

Materials

Lesson 1 Exit Ticket (M-A2-7-1_Lesson 1 Exit Ticket.doc and M-A2-7-1_Lesson 1 Exit Ticket KEY.docx) [IS.3 - Struggling Learners]
Lesson 1 Graphic Organizer (M-A2-7-1_Lesson 1 Graphic Organizer.doc)
Absolute Value Worksheet (M-A2-7-1_Absolute_Value_Worksheet.docx and
M-A2-7-1_Absolute_Value_Worksheet_KEY.docx)
Internet access for students

Related Unit and Lesson Plans

Related Materials & Resources

The possible inclusion of commercial websites below is not an implied endorsement of their products, which are not free, and are not required for this lesson plan.

· http://enlvm.usu.edu/ma/nav/activity.jsp?sid=nlvm&cid=4_2&lid=109

Formative Assessment

View

·         Observe students’ reasoning through the hypotheses and examples they give to assess their level of understanding.

·         During the lesson observe students’ performance on the creation of tables and graphs and defining the vertex, domain, range, and rate of change, as the details of each task reflect their engagement with each relationship.

·         Observe partner work on the creation of the real-world absolute value function and representations, as well as work on development of transformation rules. Collaboration and communication reflect higher levels of understanding.

·         Observe applet exploration (Grapher applet) to assess how well students relate to the technology.

·         Independent work on the creation of real-world absolute value functions and details, including vertex (min/max), domain, range, and rate of change indicates capacity for exploring beyond the lesson.

·         Lesson 1 Exit Ticket (M-A2-7-1_Lesson 1 Exit Ticket.doc and M-A2-7-1_Lesson 1 Exit Ticket KEY.docx) should be used with items targeted to match a wide range of student capabilities. [IS.24 - All Students]

Suggested Instructional Supports

View

Active Engagement, Modeling

[IS.23 - All Students]

W:	The implementation of active engagement, discussion, and partner and independent work will reveal student understanding of absolute value functions and transformations thereof.
H:	The brainstorming and hypotheses given, related to what an absolute value function looks like, as well as brainstorming of real-world situations, suitable for modeling by absolute value functions, provide a conceptual base from which students can pivot and excel in the lesson.
E:	The lesson is divided into two parts, with Part 1 serving as the focus or hook for the lesson and Part 2 including two in-depth and encompassing activities. Students are encouraged to develop ideas on their own, visualize functions and transformations, imagine absolute value functions in the real-world prior to exploration of examples, explore transformation of functions, in lieu of rote memorization of rules, and confirm further understanding via an applet exploration activity. The culminating requirement includes all components of the lesson, spanning creation of a real-world scenario through interpretation of the components of the function. The structure of the lesson lends itself to investigations prior to learning of definitions and rules.
R:	The encompassing short presentation on absolute value functions allows students to reflect, revisit, revise, and rethink with a partner. Students must be aware of and knowledgeable about each piece of the lesson in order to develop the short presentation. The class discussion emphasizes reflect, rethink, revise, and revisit once more.
E:	The continuous discussion requirements throughout the lesson will allow students to express understanding, ponder others’ remarks, and re-evaluate/self-evaluate their own understanding of such remarks.
T:	A variety of learning tools is included in the lesson. For example, students are provided with many visual representations, discursive opportunities, and explorations and discoveries. The ability to work with a partner at various stages of the lesson helps those students who benefit from discussion and social engagement and/or need a bit more help during the lesson.
O:	The lesson is structured in a manner whereby ideas are introduced using an inquisitive method and moves towards modeling of the idea, followed by independent work on the part of the student. The lesson emphasizes conceptual understanding of absolute value functions as a whole and asks students to visualize such functions in the real world and make authentic connections when extracting information from the function.

IS.1 - Preparation

Consider using graphic organizers (e.g., Frayer Model, Verbal Visual Word Association, Concept Circles) to introduce and review key vocabulary prior to the lesson. Other key vocabulary to consider would be functions, nonlinear functions, non-negative numbers,

IS.2 - All Students

Consider preteaching the concepts critical to this lesson, including the use of hands-on materials. Throughout the lesson (based upon the results of formative assessment), consider the pacing to be flexible to the needs of the students. Also consider the need for reteaching and/or review both during and after the lesson as necessary.

IS.3 - Struggling Learners

Consider providing struggling students with time to preview/review information on absolute value functions at www.khanacademy.org .

IS.4 - Struggling Learners

Consider using Think-Pair-Share coupled with Random Reporter to provide struggling students the opportunity to respond without fear of failure. See: www.pdesas.org/Main/Instruction .

IS.5 - Struggling Learners

Consider providing struggling students a copy of a number line which would allow them to see the distance a number is from zero or absolute value.

IS.6 - Struggling Learners

Since struggling students might not understand the significance of the V-shape for the graph of an absolute value function, consider comparing and contrasting the graph and numeric table of a quadratic function with that of an absolute value function.

IS.7 - Struggling Learners

Consider supplying struggling students a copy of this graph so that the focus can be on the characteristics, not the act of graphing the function.

IS.8 - All Students

Consider making the connection between the numeric table and graph of the function explicit. For example, show/discuss the rate of change in the table and how it shows up in the graph of the function.

IS.9 - All Students

Consider asking questions that assess and/or advance student understanding of the negative numbers in relationship to the context of the problem.

IS.10 - All Students

Consider providing a sketch of a coordinate system with appropriate scales (y-axis: [-10, 200] and x-axis: [-5, 5]) for the task. This provides the student an opportunity to use smaller steps as he/she learns how to graph absolute value functions.

IS.11 - All Students

Consider revisiting how to read the graph of a function (“left to right”). This will ensure students understand how the function’s relationship shows a decrease and increase in distance.

IS.12 - All Students

Consider a brief review of rate of change (from their understanding of linear functions) prior to this activity.

IS.13 - Struggling Learners

Consider providing struggling students one or two examples of absolute value functions in several representative forms (words, graph/picture, numeric table, and algebraic expression) prior to having them imagine a real-world situation on their own.

IS.14 - All Students

A possible option is to have students focus on one type of transformation (ie horizontal shifts, vertical shifts, dilations or reflections) at a time. This provides students an opportunity to deepen their understanding and make connections with transformations from previously learned parent functions.

IS.15 - Struggling Learners

Using the graphic organizer (M-A2-7-1_Lesson 1 Graphic Organizer.doc) at this time would be beneficial to struggling students because it provides a way to organize and visually see the connections between numeric tables, graphs and the transformations to the parent function.

IS.16 - All Students

Consider writing a rule for each type of transformation (horizontal shift, vertical shift, reflection or dilation) directly after the student focuses on that specific transformation. This provides an opportunity to anchor the development of the concept before moving onto another type of transformation.

IS.17 - Struggling Learners

For the struggling student, consider reviewing domain, range and rate of change using a known function (linear) before finding the absolute value’s range, domain and rater of change information. This connection with previous learning strengthens the previous learning and provides an opportunity to transfer the knowledge to the new situation.

IS.18 - Struggling Learners

It may be beneficial to complete this activity in groups (small or large) so that struggling learners may communicate with others and benefit from the thinking processes that are shared. Be sure that conversations are facilitated within the group(s) so that student thinking is shared.

IS.19 - All Students

Consider using multiple forms of representing an absolute value function (graphs, numeric tables, and algebraic expressions) and making the connections between the different forms explicit as a way to reinforce the understanding of rate of change for an absolute value function.

IS.20 - All Students

IS.21 - All Students

Consider providing a graphic organizer (with column headings: algebraic form of function, graph of function, vertex, domain, range, , rate of change, and observations) for the students to record notes and provide observations while they use the applet.

IS.22 - All Students

Consider viewing “Supporting Students Through a Wrap-Around Instructional Plan” (Marjory Montague) on www.naset.org .

IS.23 - All Students

Also consider Think-Pair-Share, Random Reporter, Think Alouds, Math Journal, and use of graphic organizers.

IS.24 - All Students

Consider viewing the publication, Teachers ‘Desk Reference: Essential Practices for Effective Mathematics Instruction in order to review the sections on formative assessment as well as assessing and advancing questions. This publication can be found at: http://www.pattan.net/category/Resources/PaTTAN%20Publications/Browse/Single/?id=4e1f51d3150ba09c384e0000

Instructional Procedures

View

Part 1

Students will hypothesize what they believe an absolute value function looks like. Ask students to pull from prior knowledge the definition of absolute value (i.e., the distance a number is from zero). [IS.4 - Struggling Learners] With a function, each and every input has one and only one output. Therefore, if the number 2 is two units from 0, then −2 is also two units from 0. [IS.5 - Struggling Learners] Thus, both x-values of −2 and 2 have an output value of 2. Students might suggest making a table of values to investigate the relationship.

x	y = \|x\|
−3	3
−2	2
−1	1
0	0
1	1
2	2
3	3

Students should notice that the y-values are all positive, thus the graph will be in the shape of a V, opening up. Students should also note the origin is at (0, 0). Ask students to plot the ordered pairs, using the table above. [IS.6 - Struggling Learners]

Students should help create the graph below. [IS.7 - Struggling Learners]

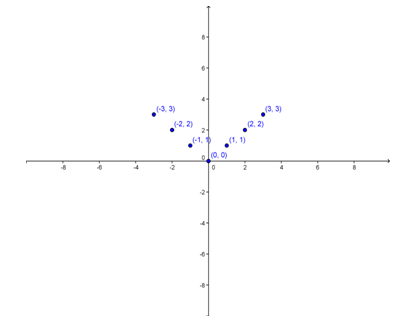
Review with students that the points should be connected to demonstrate the function.

Doing so will create the graph below. [IS.8 - All Students]

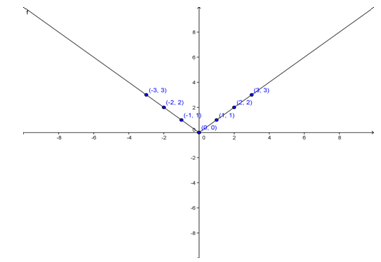
Take one of the examples and model with a table and graph.

Sample problem:

Joseph is traveling home for the weekend. He wants to model the miles he is away from home, both prior to his arrival and following his departure, for each hour that passes. [IS.9 - All Students] [IS.10 - All Students]

Hours (Prior to Arrival and Following Departure)	Miles Away
−2	120
−1	60
0	0
1	60
2	120

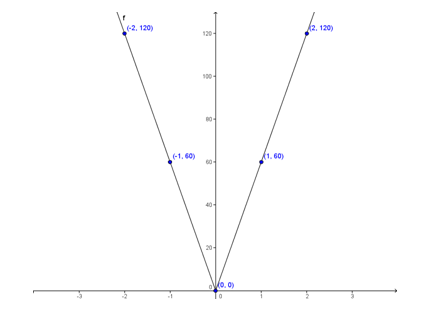
It can be noted that the distance decreases, reaches zero, and then increases. [IS.11 - All Students] From negative 2 hours (or 2 hours prior to arrival) to arrival at the destination (modeled by the origin (0, 0)), the graph decreases at a steady rate. There is a constant rate of change. From departure from the destination (again modeled by the origin (0, 0)), the graph increases at a steady rate. Again, there is a constant rate of change of 60 for each hour that passes. [IS.12 - All Students]

The vertex of the absolute value function is also the origin (0, 0). In this real-world context, the vertex, or minimum, relates to the destination (i.e., time is zero and mileage is zero). Joseph isn’t traveling anymore, thus there is not any time or mileage recorded. The vertex is at (0, 0), which shows the function is not shifted right or left or up or down.

It is easy to see that this type of real-world scenario should be modeled by an absolute value function, which is a nonlinear function.

Ask students to imagine a real-world situation that might involve an absolute value function. [IS.13 - Struggling Learners]

Examples might include distance from school and time taken, both walking to and from the school; mileage driven and hours taken etc. (distance and time problems)

For example, a student walks one mile to school each morning and one mile home each afternoon and takes 15 minutes in each direction. If the time prior to the student’s arrival at school is –15, what numbers represent the student’s arrival at school and arrival at home? (0, 15).

Place each student with a partner and have the group create a real-world absolute value function, table of values, and graph. Ask students to be as specific about all of the details of the graph and table as possible. How do they relate to the problem? How do you describe them in everyday language?

Part 2

Activity 1: Absolute Value Parent Function and Variations Thereof

Expose students to the absolute value parent function and transformed absolute value functions. A parent function is a function that has not been transformed. [IS.14 - All Students]

See examples below:

y = |x|

y = 2|x|

y = –|x|

y = –2|x|

y = |x| + 2

y = |x + 2|

y = |x| – 2

y = |x – 2|

Have students investigate transformations with tables and graphs. Prior to creation of each representation, have students ponder what would happen to the output and graph with each transformed equation.

[IS.15 - Struggling Learners]

For each of the previous examples, students might guess that the graph is narrower or wider, reflected across one of the axes, narrower or wider and reflected across one of the axes, and shifted up or down 2. Students might have difficulty with the transformation within the absolute value bars, y = |x + 2|and y = |x – 2|. Students may believe these are transformations upward or downward, or switch the direction of the shift left or right. In order to confirm and disprove these guesses, have students create a table of values and graph for each.

Next, have students compare the graphs and tables and also compare the graphs with the equations. What happened? Why did such a transformation come about? Why did y = |x + 2|result in a shift of the parent function two units to the left? Why did y = |x – 2|result in a shift of the parent function two units to the right?

Students should compare the tables, graphs, and equations in order to answer these questions.

Function

Table

Graph

y = |x|

x	y = \|x\|
−3	3
−2	2
−1	1
0	0
1	1
2	2
3	3

y = |x + 2|

x	y = \|x + 2\|
−3	1
−2	0
−1	1
0	2
1	3
2	4
3	5

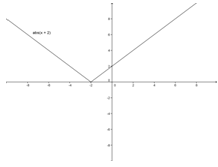
y = |x + 2|

x	y = \|x + 2\|
−3	5
−2	4
−1	3
0	2
1	1
2	0
3	1

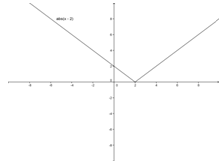
By examining the output or y-values, students can see that the y-values caused the graph to shift to the left two units for y = |x + 2|and shift to the right two units for y = |x – 2|. With y = |x + 2|, the y-values decreased by 2 until the x-value of −1. Then, the y-values increased by 2 after that. With y = |x – 2|, the y-values increased by 2 until the x-value of 1. Then, the y-values decreased by 2 after that. The main point to notice is that the vertex transformed from (0, 0) with y = |x|to (−2, 0) with y = |x + 2|and (2, 0) withy = |x – 2|. Hence the reasoning for the shift to the left of two units with y = |x + 2|and shift to the right of two units withy = |x – 2|.

Hand out copies of the Lesson 1 Graphic Organizer (M-A2-7-1_Lesson 1 Graphic Organizer.doc).

The graph with each function illustrates the left and right shifts. Note that the lines for
abs(x + 2), abs(x), and abs(x–2) are red, black, and green respectively.

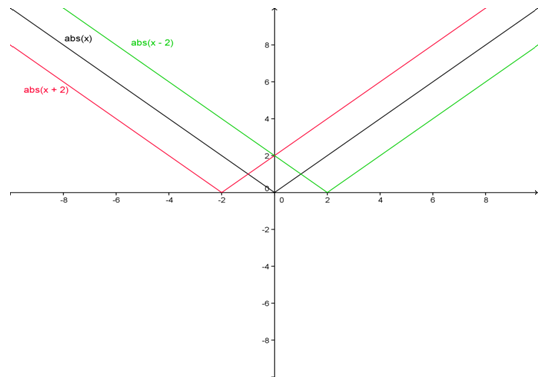
“Let’s try to write some rules about transformations of absolute value functions.”

Have students work with a partner to write rules, regarding transformations. [IS.16 - All Students] As a class, discuss the rules and create the chart below.

“When comparing graphs of absolute value functions with the parent absolute value function y = |x|note the following”:

y = |x – a|

y = |x| + a

y = a|x|

If a is > 0, the graph is a units to the right of the graph of y = |x|.

If a is < 0, the graph is a units to the left of the graph of y = |x|.

If a is > 0, the graph is a units above the graph of y = |x|.

If a is < 0, the graph is a units below the graph of y = |x|.

If |a| > 1, the graph is narrower than the graph of y = |x|.

If 0 < |a| < 1, the graph will be wider than the graph of y = |x|.

When a is positive, the graph opens up. When a is negative, the graph opens down.

In examining a sampling of the graphs from before, namely, y = |x|, y = |x + 2|and y = |x| – 2, let’s find the domain and range of each. Let’s also determine the rate of change. [IS.17 - Struggling Learners]

The domain of a function is the set of x-values or input values. The range of a function is the set of y-values or output values.

y = |x|

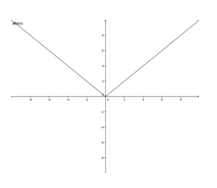
The domain of the function y = |x|is all real numbers or (−∞, ∞).

The range of the function y = |x|is all non-negative real numbers or [0, ∞).

The graph shows the x-values to span infinitely in both directions, thus including all reals. The graph also shows the y-values to span infinitely above and including the value of 0.

y = |x + 2|

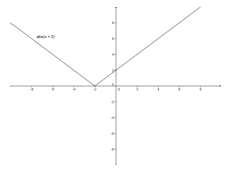
The domain of the function y = |x + 2|is all real numbers or (−∞, ∞).

The range of the function y = |x + 2|is all non-negative real numbers or [0, ∞).

The graph shows the x-values to span infinitely in both directions, thus including all reals. The graph also shows the y-values to span infinitely above and including the value of 0. Note that the domain and range for this transformed absolute value function is the same as the parent absolute value function.

y = |x| – 2

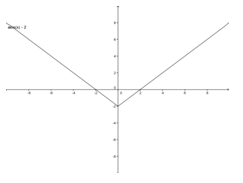
The domain of the function y = |x| – 2 is all real numbers.

The range of the function y = |x| – 2 is all real numbers greater than or equal to −2 or
[−2, ∞). The graph shows the x-values to span infinitely in both directions, thus including all reals. The graph shows the y-values to span infinitely above and including the value of −2.

Use the Absolute Value Worksheet (M-A2-7-1_Absolute_Value_Worksheet.docx and
M-A2-7-1_Absolute_Value_Worksheet_KEY.docx) to give students more practice with absolute value functions. [IS.18 - Struggling Learners]

“How can the rate of change be determined?”

For the absolute value parent function, the rate of change is −1 up until the origin. The rate of change is then 1. [IS.19 - All Students] Note: The rate of change is synonymous with slope.

Fory = |x + 2|, the rate of change is −1 up until the vertex. The rate of change is then 1.

Fory = |x|– 2, the rate of change is again −1 up until the vertex. The rate of change is then 1.

Have students find the domain, range, rate of change, and vertex for other transformed functions.

What Does a Reflection Look Like?

“Can we reflect an absolute value function across the x-axis? Certainly. This function is written in the form y = –|x|. What happens to the y-values in such a transformation? Correct, the y-values are negated. Thus, the graph is reflected over the x-axis. Let’s take a look.”

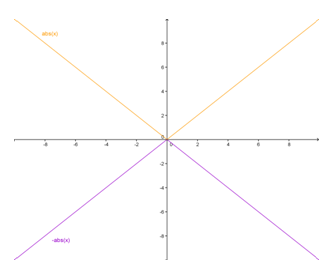
Note that the graph lines for –abs(x) and abs(x) are purple and orange respectively.

Ask students to make a table of values and graph the following absolute value functions:

y = 4|x|

y = –4|x|

y = |x – 4|

y = –|x – 4|

Activity 2: Exploring with a Virtual Grapher [IS.20 - Struggling Learners]

Have students explore absolute value functions and transformations of functions using NLVM’s virtual Grapher applet available at http://enlvm.usu.edu/ma/nav/activity.jsp?sid=nlvm&cid=4_2&lid=109.

Students should use the applet to explore the parent function y = |x|and transformations, including reflection across the x-axis, y = –|x|. Students should develop skills in other transformations, such as translations to right, left, up, and down. By exploring and discovering with the applet, students should record notes and observances, [IS.21 - All Students] related to connections between the function equation and resulting graph. Have students explore min/max (vertex), domain, range, and rate of change. Students should also use the applet to explore the changes in the width of the function when varying the value of the coefficient of a.

Students will be asked to imagine an absolute value function that represents a new real-world scenario. They should create a table of values and a graph to illustrate the function. Students should explain the rate of change and meaning of the vertex of the graph in the context of the problem. They should also note the meaning of the domain and range within the context of the problem.

For review, ask students to create a short presentation relating the parent function and other absolute value functions. [IS.22 - All Students] Ask students to focus on making connections and illuminating the conceptual underpinnings of working with these types of functions. The primary focus of the lesson should be knowledge and understanding of when such modeling with absolute value functions is appropriate; ways to extract information from the equation, table, and graph; and how to verbalize the findings in a manner that relates directly to the context of the problem. Provide time for discussion at the close of the presentations.

Provide students with the Lesson 1 Exit Ticket (M-A2-7-1_Lesson 1 Exit Ticket.doc) and assign items accordingly by appropriate difficulty.

Extension:

· Explore x-and y-intercepts of absolute value functions. In addition, provide more difficult functions that include a combination of transformations. Examples include: y = –3|x – 6| + 4,
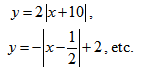, etc.

· Include examples of absolute value functions that use more difficult numbers, such as fractions and decimals.

Absolute Value Functions