After this lesson, students will know what a polynomial is and will understand that polynomial functions are another way to represent real-world situations. They will see the link between their previous knowledge of linear and quadratic functions and polynomial functions. They will know vocabulary such as degree, binomial, and trinomial. Students will build upon this knowledge in Lesson 2 and will learn to use polynomial functions to represent real-world situations. [IS.9 - All Students] Students will be able to write polynomials in standard form and classify polynomials by degree and number of terms. They will be able to graph polynomials in factored form because they will understand the connection between the number of roots and the degree of the polynomial.
To introduce the lesson, activate students’ prior knowledge. Place the following problems on the board.
-
1. 3x + 4x
-
2. 5x2 − 3x2
-
3. 7x + 2x2 − x + 8x2
“What does it mean to combine like terms?”
Write the following on the board:

“If we can’t combine the terms, then we should arrange them in an order that makes sense. Does anyone have an idea of how to rearrange the terms?”
If students don’t volunteer any ideas, ask, “How are books sorted in the library? How are words sorted in a dictionary? What does it mean to put a list in ‘descending’ order? [IS.10 - Struggling Learners] Try putting the terms that are on the board in descending order.”
Students will probably come up with the following:
-
5x4 + 4 + 3x2 − x − 2x3 (put the coefficients in descending order)
-
5x4 + 4 + 3x2 − 2x3 − x (put the coefficients in descending order, ignoring signs)
-
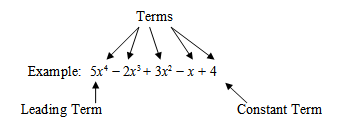
5x4 − 2x3 + 3x2 − x + 4 (correctly put the terms in descending order)
Tell the students who wrote the last expression that they have just written a polynomial in standard form.
Hand out the Polynomial Functions Graphic Organizer (see M-A2-3-1_Polynomial Functions Graphic Organizer in the Resources folder). Below is what students should add to their graphic organizers.
-
Polynomial: A sum of terms that has variables that are raised to whole-number exponents.
- Quadratic, in this context, means to the second power (Latin: quadratum is square, as area of a square).
-
Coefficient: The number that is being multiplied by the variable; the number in front of the leading term is called the leading coefficient.
-
Zero degree: constant (example: 5).
-
Monomial: a polynomial that has one term (example: 4x)
-
Binomial: a polynomial that has two terms (example: 4x − 3)
-
Trinomial: a polynomial that has three terms (example: 2x2 + 4x − 3)
-
Any term with four or more terms is a polynomial.
-
First-degree: also known as “linear” (example: 5x + 1)
-
Second-degree: also known as “quadratic” (example: 9x2 − 5x + 3)
-
Third-degree: also known as “cubic” (example: 4x3 +2x2 − x + 8)
-
Fourth-degree: also known as “quartic”
-
(example: 8x4 − 5x3 + 6x2 + x − 3)
-
(example: x5 + 2x4 – 5x3 – x2 + 8x + 4).
-
Polynomial equations of degree greater than five are not solvable by methods other than approximations.
Activity 1 (Auditory): Defining Polynomials
Individually students should write two polynomials in standard form on an index card and hand it in. Read aloud one polynomial at a time and ask students to answer the following questions:
-
“Is it a polynomial?” (some students may not have written one correctly)
-
“What degree polynomial is it? Classify it as linear, quadratic, cubic, quartic, or none of the above.”
-
“How many terms does the polynomial have? Classify it as a monomial, binomial, trinomial, or none of the above.”
Activity 2 (Auditory): Writing Polynomials in Standard Form
Using the index cards and the polynomials that were not used in Activity 1, read aloud the polynomials not in standard form.
-
“Write the polynomial in standard form.”
-
“What is the polynomial’s degree?”
-
“How many terms does the polynomial have? So what is its name?”
-
“Pair up and check each other’s work.”
Activity 3: Think-Pair-Share
On large graph paper on the board, post one graph of a line and one graph of a parabola (examples: y = x − 2 and y = (x + 1)2 − 4). “With your partner, write the equations of each graph. Use what you have learned today to write them.” Ask pairs to share their answers and how they came up with their equations.
“Does anyone see a link between the graphs and his/her equations? What does the equation say about the graph?”
Remind students that plotting the graph without a graphing calculator means substituting values for x and marking the corresponding f(x) as an ordered pair, and then continuing to plot a sufficient number of points to complete the graph.
If students struggle, say, “Look at your graphic organizer. What were some things you learned today about polynomials?”
After a few more minutes, have one partner from each pair come up. Tell the partners: “Look at where the graph crosses the x-axis and look at the degree of the polynomial.” Students will take this information back to their partners and try to make the connection. Make sure the quadratic function used as an example has two x-intercepts.
After a few minutes, choose a few volunteers to give their opinion of the connections. Some students are likely to have realized that the degree of the polynomial is the same as the number of roots (x-intercepts) of the graph.
Activity 4: Think-Pair-Share
Before thoroughly explaining the concept, put a graph of a cubic function and the graph of a quartic function on the board. “Individually, find the roots (x-intercepts) of the graphs. When you have written them, discuss the roots with your partner and the degrees of each graph. How are they linked?” If some pairs need opportunity for additional learning, place them with a pair that understands the concept. As a whole class, pairs can share their conclusions about polynomials’ degrees and the number of roots that the graphs have.
Activity 5: Pairs
In pairs, one student gives the degree and the number of terms and the second student writes a polynomial in standard form with that same degree and number of terms. The first student checks the work and either agrees or explains why it’s incorrect. Once they agree, they switch roles.
Activity 6: Whole Class
Write the following terms on sheets of paper and tape them to the board.
5x4 −8x5 −3x3 −x 6 4x2 −7x2 5x 6x4
2x3 10x3 x2 −3x 1 5 6x −2x2 −3
“Let’s make four polynomials with these 18 terms. That means we will not be combining like terms. Put the polynomials in standard form. You will be coming up to the board one or two at a time to move one term. Those who are sitting in their desks should remain quiet and not help the students who are at the board. If there is not a negative sign in front of a term, use the plus sign. Once every term is in a polynomial we will look at each one and check that it is in standard form. If it is, we will classify the polynomial by degree (including whether it’s linear, quadratic, etc.) and how many roots the polynomial should have.”
During this activity, you can tally how many students got their term correct and how many didn’t, just to gauge how well the class understands.
It’s easy to duplicate this activity and repeat it with different sets of terms and it may be useful to customize the individual elements to suit the needs of individual students or a particular class.
Use the Lesson 1 Exit Ticket (M-A2-3-1_Lesson 1 Exit Ticket.doc and M-A2-3-1_Lesson 1 Exit Ticket KEY.doc) for a quick way to evaluate whether students understand the concepts. Have students fill out the table on the Lesson 1 Exit Ticket. “The number of roots can be used to find the degree of polynomial equations, and in the next lesson we will be using roots to determine the factors of polynomials.”
Extension:
-
(3x − 1)(x2 + 4x − 21)
-
(−2x + 4)(x − 2)
-
(x + 3)(x3 + 2x2 − x + 4)
-
Answer the following questions for each exercise:
-
A. What is the degree of each polynomial?
-
1. Linear, quadratic
-
2. Linear, linear
-
3. Linear, cubic
-
B. Multiply the two polynomials using area models and simplify your answer (write in standard form).
-
1. 3x3 + 11x2 – 67x + 21
-
2. –2x2 + 8x + 8
-
3. x4 + 5x3 + 5x2 + x + 12
-
C. What is the degree of your polynomial?
-
1. Cubic
-
2. Quadratic
-
3. Quartic
-
D. How many real roots should your polynomial have?
-
Cubic: 3; Quadratic: 2; Quartic: 4
