After this lesson, students will know what the factor theorem is and how it relates roots to factors. They will understand how synthetic division shows when a value is a root of a polynomial and that synthetic division produces the same results as long division but is much easier and quicker. This lesson builds on the basics of polynomials and introduces characteristics of a polynomial’s graph. Students need to understand where roots come from and will use their knowledge of roots in the application of polynomial functions in real-world situations. Students will be able to use synthetic division to determine if a value is a root. They will be able to write polynomial equations knowing the roots and write polynomials in factored form.
Have students look at the graph of a parabola (for example: y = x2 + 2x − 3). Then have students answer the following questions:
-
“What is the degree and how many x-intercepts does the graph have? (Refer to the fundamental theorem of algebra)”
-
“What are the zeros or x-intercepts?”
-
“What is the equation of the parabola in factored form?”
-
“What connection is there between the factors and zeros?”
“Since x2 + 2x − 3 = (x + 3)(x − 1), that means 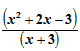 = x − 1. We use division of polynomials to help determine the roots of the polynomials. How do we divide polynomials? We can use what we know from long division, or we can take the shortcut and use synthetic division.”
= x − 1. We use division of polynomials to help determine the roots of the polynomials. How do we divide polynomials? We can use what we know from long division, or we can take the shortcut and use synthetic division.”
Long Division:
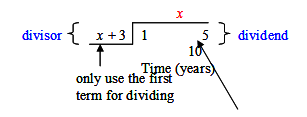
-
Step 1: x2 divided by x = x (line up like terms) (x² / x) = x
-
Step 2: Multiply x by x + 3 and write the product underneath the dividend.
-
Step 3: Subtract the product by distributing the negative sign across all terms in the product.
-
Step 4: − x divided by x = − 1 or (−x / x) = −1
-
Step 5: Multiply − 1 by x + 3 and write the product underneath; then subtract.

[IS.6 - Struggling Learners]
- Step 5
- Second Example of Long Division:
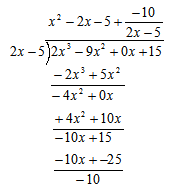
“This process is like long division. We are going to use an easier process called synthetic division for dividing polynomials.”
“There is one requirement in order to use synthetic division: The divisor has to be of the form x − a or x + a. Using the same example from above, divide x2 + 2x − 3 by x + 3.”
The following notes should be displayed on the board for students to copy.
Step 1: Write the coefficients of the dividend (the numbers in front of the variables and the constant: 1, 2, − 3) and draw an “L” around the numbers as well as a dashed line in front of the constant (optional).
Step 2: Since the divisor is x + 3, because x + 3 = 0 and x = –3, we are going to use − 3 for synthetic division. Place − 3 on the left side of the 1 on the other side of the line.
-
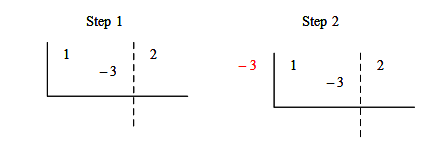
Step 3: Bring down the 1. (Always bring down the first coefficient.)
Step 4: Multiply the 1 by the divisor − 3 and place the product under the 2.
-
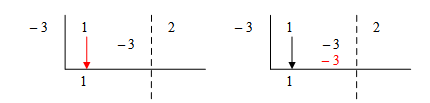
Step 5: Add 2 + −3 and write the sum under the line.
Step 6: Multiply the − 1 by the divisor − 3 and place the product under the − 3.
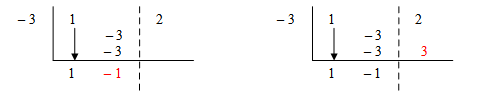
Step 7: Add − 3 + 3 and write the sum under the line.
Step 8: Write out the quotient. The number on the right of the dashed line is the remainder. The first number to the left of the dashed line is the new constant, the next number is the coefficient in front of x, and if there were one more number, it would be the coefficient in front of x2 and so on. This process can be used with third, fourth, and larger degree polynomials as long as the divisor is of the form x ± a.
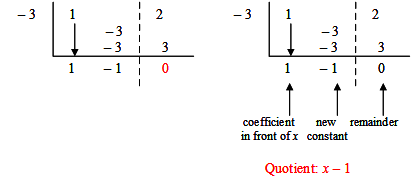
[IS.7 - Struggling Learners]
- Third example for synthetic division:
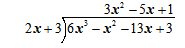
Note: In Step 2, explain that in synthetic division you use the opposite of the sign in the divisor. Remember that the sum of the constant term and its additive inverse must be zero. Our divisor was x + 3, so in synthetic division it needs to be − 3. If we had a divisor of x − 4, we would use + 4. Stop and see if anyone has any questions at this step.
Activity 1: Group Work
If the classroom has whiteboards on all four walls, write the following division problems on the boards. If the room doesn’t have whiteboards all the way around, place the problems on poster paper and hang them around the room.
-
Long Division: 1.(x3 + x2 − 5x − 2) ÷ (x − 2)
-
2. (x2 + 2x + 1) ÷ (x + 1)
-
3. (x3 − 3x2 − 11x + 5) ÷ (x2 + 2x − 1)
-
4. (x4 + 4x3 + 6x2 + 4x + 1) ÷ (x + 1)
-
Answers: 1. x2 + 3x + 1
-
2. x + 1
-
3. (x – 5)
-
4. x3 + 3x2 + 3x + 1
-
Synthetic Division:
-
5. (9x3 − 6x2 − x +30) ÷ (x − 3)
-
6. (x2 − 3x − 28) ÷ (x + 4)
-
7. (x3 − x2 − 2x) ÷ (x + 1)
-
8. (x3 + 7x2 − 38x + 40) ÷ (x − 2)
-
9. (x4 + 3x3 − 25x2 + 33x + 72) ÷ (x + 6)
-
10. (x2 + x − 72) ÷ (x − 8)
-
Answers: 5. (9x2 + 21x + 62) + (216 / x – 3)
-
6. (x – 7)
-
7. (x3 – 2x)
-
8. (x2 + 9x – 20)
-
9. (x3 – 3x2 – 7x + 75) – (378 / x + 6)
-
10. (x + 9)
-
Split the class into groups of three to four and have each group go to a problem on the board. Have students work on the problem in front of them for one to two minutes. If they finish the problem in that time, they should raise their hands and have you check their work. If they are right, they should erase their work so the next group doesn’t see it. If they do not finish the problem, that’s okay. After time is up, have the class rotate clockwise. The groups then have to look at the next problem and see if the group in front of them was on the right track to solve the problem. The current group finishes the problem and gets the work checked. Repeat this process for 10 to 15 minutes, making sure each group has seen at least one long-division problem and about four to five synthetic-division problems.
Bring the class back together. Ask, “Which process did you like better and why?”
Most likely they will ask why synthetic division works. This is a good time to introduce the Factor Theorem. “Since polynomials can be used to model real-world applications, it is important to determine the x-intercepts for information about the real-world situation.”
Put the following on the board for students to copy in their notes.
-
Factor theorem: If a is used to synthetically divide a polynomial and it produces a remainder of zero, then not only is x = a a root of the polynomial, but x − a is a factor of the polynomial.
-
In the previous example, −3 was used in synthetic division with the polynomial x2 + 2x − 3 and it produced a remainder of 0; therefore, x − (−3) or x + 3 is a factor of the polynomial.
“Synthetic division is a step-by-step process where each step gives information that is useful for the next step. In that way, it builds upon itself.”
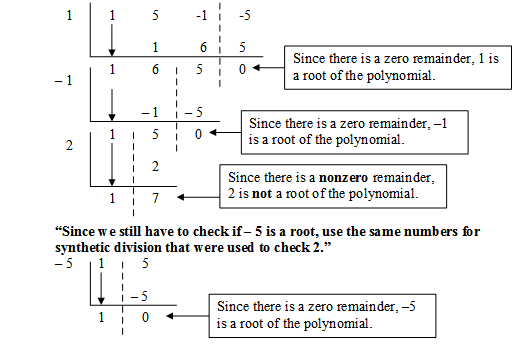
Example: Determine which of the following are roots of the polynomial x3 + 5x2 − x − 5: 1, − 1, 2, and − 5.
Example: (x3 – 5x– 4) ÷ (x – 3)
3 1 0 –5 –4
3 9 12
1 3 4 8
Answer: x2 + 3x + 4 + ( 8 / x – 3 )
Activity 2: Pairs
Place the following table on the board and discuss with the class the middle column.
-
|
Polynomial
|
Number of Roots the Polynomial Should Have
|
Possible Roots
|
|
x3 + 3x2 − 6x − 8
|
|
2, 1, − 4, − 1
|
|
x4 − 34x2 + 225
|
|
−5, 5, 3, − 3, 2
|
|
x2 + 3x − 28
|
|
4, − 7, 6
|
|
x2 + 2x
|
-
|
-
0, − 2, 3
|
“With your partner, you are going to determine which numbers are roots and which numbers are not roots. You should use synthetic division as in the previous example. In the second polynomial, you will need to use a coefficient of 0 for the x3 and x terms.”
-
|
Polynomials
|
|
1
|
x3 + 6x2 + 5x G
|
|
2
|
x2 − 7x + 6 E
|
|
3
|
x4 − 7x3 − 7x2 + 43x + 42 F
|
|
4
|
x2 − 10x + 16 B
|
|
5
|
x4 + 4x3 − 53x2 − 168x C
|
|
6
|
x5 + x4 − 51x3 + 31x2 + 538x − 840 H
|
|
7
|
x2 + 10x + 24 A
|
|
8
|
x3 − 15x2 + 74x − 120 D
|
|
|
Roots
|
|
A
|
−4, −6
|
|
B
|
2, 8
|
|
C
|
−3, −8, 0, 7
|
|
D
|
4, 5, 6
|
|
E
|
1, 6
|
|
F
|
−2, 7, −1, 3
|
|
G
|
−5, −1, 0
|
|
H
|
3, −7, 2, −4, 5
|
-
-
-
Walk around and check students’ work. Have students who are catching on quickly write the polynomials in factored form. From the previous example, if they determine that −1, 1, and −5 are roots of the polynomial x3 + 5x2 − x − 5, then they can write the roots as factors: x3 + 5x2 − x − 5 = (x + 1)(x − 1)(x + 5). Choose a couple of groups to write their work on the board. This is a good way for students to check their work and ask questions.
Activity 3:
“Individually come up with your own polynomials by following these steps:
-
Think of three to five numbers to be the roots of a polynomial.
-
Write those roots in factored form.
-
Multiply all the factors together to create a polynomial in standard form.”
Next, have students pass their polynomial to the student behind them along with two of the roots and a number that is not a root. Students then have to determine the roots and the nonroots. When everyone is finished, students pass their work back to the person in front of them to check for errors.
Another example: (x + 7)(x – 6)(x – 11)
x3–10x2–53x + 462 possible roots, –2, –1, 1, 2
Use the Lesson 2 Exit Ticket (see M-A2-3-2_Lesson 2 Exit Ticket and M-A2-3-2_Lesson 2 Exit Ticket KEY in the Resources folder) to evaluate students’ understanding.
Use synthetic division to match the polynomials on the left with their roots on the right.
Extension:
-
x2 – ax + 3x – 3a (x + 3)
-
x2 – ax – 5x + 5a (x – 5)
-
x2 – ax + bx – ab (x + b)
-
x2 – ax – bcx + abc (x – bc)
-
6x3 – x2 – 13x + 3 (2x + 3)
