W:This lesson connects the student’s previous experience with systems of equations to the new concept of systems of inequalities. Although students discovered that solving systems of equations is often most efficient when done algebraically, they will find that solving systems of inequalities by graphing is the most common (easiest) approach conceptually. Students will solve systems of two inequalities using linear programming and progress to graphing systems of three or more inequalities. Students will measure attributes of the geometric shapes that are created by graphing these inequalities.
H:“Remember the problem of the movie ticket prices from the previous lesson? ‘The local movie theater was celebrating its 25th anniversary and was giving a discount on tickets. You didn’t know what the ticket prices were, but you heard two of your classmates discuss how much it cost their families to go to a movie last weekend. One student said the cost for two adults and two children was $12. Another student said the cost for three adults and four children was $20.’”

“What would change in the equations if you overheard your first classmate say that she couldn’t remember the exact total, but for two adults and two children it was $12 or less? The second student couldn’t remember the exact total either, but for three adults and four children, it was $20 or less.”
“What would the system look like now? Have any of the numbers changed?
If the numbers didn’t change, how did the equation change?”
Allow students to work in groups to solve the problem. Let them know that students will be randomly called on for all groups to present their solutions to the class (Random Reporter method).
When groups have presented, they should take notes on the lesson. For learners who will be distracted by note taking, hand out a copy of the notes to allow more focus on the verbal descriptions and instructions of the teacher.
E: Have students practice graphing inequalities (A1-5-3_Graphing Inequalities Worksheet.docx).
The followingnotes should be displayed on the board for students to copy:
Graphing Systems of Linear Inequalities
Example 1:
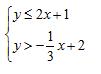
In the Graphing Inequalities Worksheet, highway signs tell us to drive as fast or faster than 40 miles per hour and no faster than 65 miles per hour. The number line between 40 and 65 shows the inequality in one dimension (straight line) and two directions (left and right). Similarly, the two inequalities in this system have two dimensions (x-axis and y-axis) and four directions (left, right, up, down).
(End of student notes.)
Step 1: If the inequalities are not in slope-intercept form, convert them so that they are.
The first equation is already in slope-intercept form, but the second equation needs to be changed.
Put the following notes on the board for students to copy.
***Remember if you divide both sides by a negative number, the inequality sign flips.
Step 2: Graph the inequalities as if they were equations.
a. If the inequality is ≥ or ≤, graph a solid line because we want to include all of the points along the line.
b. If the inequality is > or <, graph a dashed line because we want to use it as a boundary without including the points directly on the line.
In this example, one line is solid (>) and one line is broken (≤). The lines drawn are the borders for the solution set.
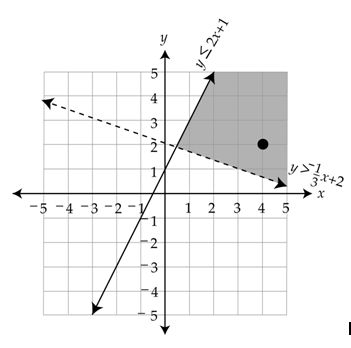
Step 3: Shade the solution set. Since this is a system of linear inequalities, there is not going to be just one answer. All the coordinates that satisfy the system of inequalities are part of the solution set. Pick a test point (that is not on either one of the lines) to determine which side of the lines to shade.
a. If the test point satisfies both inequalities, shade the area in which the test point lies.
b. If the test point does not satisfy both inequalities, pick another area that the lines border and pick another test point.
In this example, pick the test point (4, 2).
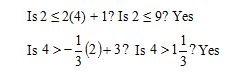
Since the test point satisfies both inequalities, shade the bordered area that includes the point (4, 2) .
(End of student notes.)
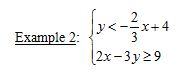
Note: This solution must be shown graphically. [IS.2 - All Students]
Step 1: If the inequalities are not in slope-intercept form, convert them so that they are.
The first equation is already in slope-intercept form, but the second one needs to be changed.
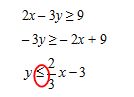
Notice that the inequality sign was reversed.
“Can anyone explain why?”(because we divided both sides by a negative number)
Step 2: Graph the inequalities as if they were equations.
a. If the inequality is ≥ or ≤, graph a solid line. “Who can explain why?”
b. If the inequality is > or <, graph a dashed line. “Who can explain why?”
In this example, the first line is going to be dashed and the second will be solid.
Step 3: Shade the solution set.
a. If the test point satisfies both inequalities, shade the area in which the test point lies.
b. If the test point does not satisfy both inequalities, pick another area that the lines border and pick another test point.
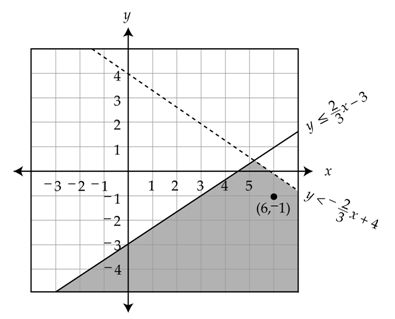
In this example, pick the test point (0, 0).
Is 0 < –⅔(0) + 4? Is 0 < 4? Yes
Is 2(0) – 3(0) ≥ 9? Is 0 ≥ 9? No
Since the test point only satisfies the first inequality, we need to pick a new test point. Pick a point that is on the same side of the dashed line as the previous test point, but on the opposite side of the solid line from the previous test point. Try
(6, -1).
If no student has noticed that the graphs of > are always shaded above the line and < below the line, ask the question: “Has anyone noticed a faster way to know which side of the line to shade?” Sometimes students may misunderstand which is “above” or “below,” especially when the line has a steep slope.
E: Give students the following four systems to solve. They can either work alone or in pairs.
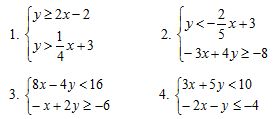
Go over the solutions as a whole class.
“The opening problem (the movie ticket prices) introduces us to a concept called linear programming. Linear programming is a technique for determining the way to the best outcome given a few constraints (example: maximizing profits or minimizing costs).”
“What changed in the problem when students said the movie cost exactly $12 and $20 to the movie cost $12 or less and $20 or less? The equations became inequalities.” 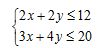
“We could graph these inequalities now, but remember that x and y represent prices. That means there are two more constraints to add to the system. Since movie theaters cannot sell tickets for less than $0, we will add the following two inequalities: x ≥ 0 and y ≥ 0.”
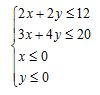
Have students graph this linear programming problem and discuss what the solution set means in terms of movie ticket prices.
“Another reason we use systems of inequalities is to measure attributes of the geometric shapes that are created by the borders of the solution set.”
Example: Let’s say the surface of a desk can be described by the following system of inequalities.
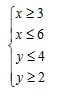
Graph the above system and determine the area and perimeter of the desk.
In pairs, have students solve for the area of the shape that is created when the following system of inequalities is graphed.
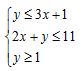
Go over the solution as a class.
R: In groups of three, have students graph the following systems of inequalities and shade the appropriate solution set. Each student graphs one border line, and students must pick a test point in different areas from one another to determine the shaded area.
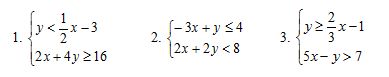
When everyone is done, have groups combine to create a larger group of six. Students should discuss and compare their work. Then as a class, discuss the graphs and whether there were any discrepancies between groups. Have students hand in their work.
E: Partner Problem:
Introduce the following problem to students. Offer the hint that they may want to determine what the x and y-variables will represent first. If they struggle with this part of the problem, help them out with it before having them move forward to complete the other steps.
Charlie works two jobs. He works 10 hours or less a week at the school’s concession stand during home athletic events. He also has a job at the local fast food restaurant where he works 20 hours or less a week. He earns $6 an hour at the concession stand and $8 an hour at the fast food restaurant. Charlie would like to earn more than $56 a week.
1. Write the system of inequalities that represents Charlie’s situation.
2. Graph the system of inequalities and shade the solution set.
3. What does the shaded area represent in terms of the hours Charlie works and the amount of money he earns?
