During the lesson, monitor students’ understanding of the following points, and adjust their understanding as necessary, to help ensure that students can master the targeted learning goals within the time frame:

• Potential energy depends on the position of an object.

• Kinetic energy derives from its movement.

• Both potential and kinetic energy are relative to the frame of reference of the observer.

• The energy involved in lifting an object will be the same as its kinetic energy when it falls the same distance.

• Friction and mechanical inefficiency will prevent you from capturing all of an object’s potential energy.

• The kinetic energy of a moving object is mass times velocity squared divided by two, or (m·v²)/2.

• The potential energy of an elevated object is mass times height times the acceleration of gravity.

Display, in a raised position, a 100 mL beaker of water, and ask, “What does this have in common with the Hoover Dam?”

The answer is that both the beaker of water and the dam represent potential energy. Both contain liquid raised to an elevated position. Released from that position, the liquid could do work. Specifically:

• Hoover Dam stops the natural flow of the Colorado River on the Nevada-Arizona border about 30 miles southeast of Las Vegas, creating Lake Meade. The lake is 180 kilometers long and contains a little more than 35 cubic kilometers of water. (That’s 35 billion metric tons of water.) From the surface of the lake on one side of the dam to the bottom of the dry canyon on the other is a drop of about 210 meters.

• The beaker of water here in the classroom has been raised about two meters (or whatever) in that frame of reference. It contains 340 grams, or a trifle more than a third of a kilogram of liquid.

Potential energy can be converted to other forms of energy, especially kinetic energy.

Next, pose this question: “What does a car going down a highway and a thrown baseball on its way to the plate have in common?”

Both possess kinetic energy, from the fact that they are in motion. Kinetic, in fact, comes from the Greek word for motion. The water in our first example will have kinetic energy if set in motion because of gravity.

Distribute copies of the Kinetic vs. Potential Energy Worksheet (S-8-7-2_Kinetic vs. Potential Energy Worksheet and KEY.doc) to students, and have them silently fill in the answers.

Lead a discussion of each item:

• water sitting in an uphill reservoir—potential

• AA battery—potential

• car moving down a highway—kinetic

• car parked on a slope—potential, since it could roll down hill

• wrecking ball hitting a wall—kinetic

• gallon of gasoline—potential as it can fuel a car

• water flowing out of a reservoir—kinetic

• coal in a mine—potential as it can be used as fuel

• debris in a road as seen by an approaching car—kinetic

The last item is a trick question intended to introduce the concept of frame of reference. Make the following point:

• Both potential and kinetic energy require a frame of reference—things are relative, in other words. For potential energy this is obvious. The water behind Hoover Dam has potential energy in the frame of reference of the generator turbines below the dam. Above the dam, the water represents no potential energy. Likewise, a moving object has kinetic energy only in the frame of reference of an observer who does not share the object’s velocity. To a car going down a highway, a crate that has fallen off a truck and is now lying in the road possesses kinetic energy. Since motion is relative, the car may as well be at rest with the crate (and road) rushing at it. But to someone standing off the side of the road, the crate has no kinetic energy at all.

“Once a frame of reference is established, potential and kinetic energy are measured much the same way. Various ways of measuring energy have been in use since humanity began harnessing energy at the start of the Industrial Revolution. The first and still most popular is the horsepower, dating to 1783. It was based on the observation that a horse harnessed to a treadmill could raise 33,000 pounds to a height of one foot in one minute.

“But this is a rather large quantity, and was based on obsolete English measure (feet and pounds.) Today we use a much smaller measure of energy, called the joule (pronounced jewel, as in diamond or ruby) named for English physicist James Prescott Joule (1818-1889).

“A joule is the energy needed to move one kilogram for a distance of one meter at an acceleration of one meter per second squared. In other words, it measures energy in terms of mass times distance moved times the force of the acceleration behind the movement.

“The contents of our water glass, meanwhile, represents potential energy because it has been placed in a position where the liquid could fall downward and perhaps do some work while falling.

“Figuring the amount of potential energy in our glass of water would seem like rocket science. Actually it’s rather straightforward. Remember, the joule represents mass times distance times acceleration. In this situation we have the three data points we need:

• Mass is a measure of the amount of H₂0 in the beaker.

• The distance moved is the distance it’s going to fall, which is the height we chose to raise it. In this case we will raise it about a foot, or about a third of a meter.

• The acceleration is the acceleration of gravity, since the mass is going to be falling. Here on the surface of the Earth that’s 9.8 meters per second squared (9.8 m/s²). If you’re stuck in an elevator and have to calculate using it, just use 10.

“So joules of potential energy equals mass times height times gravity.” Write the equation on the blackboard:

Joules =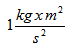

Have a student (presumably with a calculator or spreadsheet) actually perform the calculation for the glass of water, assuming it will be poured from 0.3 meters, weighs 0.34 kilograms, with an acceleration of 9.81.

The answer is 1 joule.

“How did it come to acquire this potential energy? In the case of our glass of water, we invested the muscle energy needed to raise it to that height. With Hoover Dam, the climate provided the energy needed to deposit snow on the slopes of the Rocky Mountains, which later melted, ran downstream, collected behind Hoover Dam, and formed Lake Mead.

“What does 1 joule look like?”

Have one student carefully pour the contents of the glass into another glass, while a second student holds a one meter stick so that the first glass is at approximately the proper distance (30 centimeters) above the second one. They should try to complete the act in one second.

“And that is a joule of energy.

“If we had put a pinwheel in the stream of water, so that it turned, we could say that it did work.

“And that is how Hoover Dam works, except that instead of a pinwheel it has 17 huge turbines with water hitting them at 137 kilometers per hour. The overall capacity is about 2 billon watts.

“A simpler definition is that one joule is equal to one watt of electricity for one second. In other words, a 100-watt light bulb shining for one second consumes 100 joules. Other analogies:

• The metabolism of an average person is also about equivalent to a 100-watt light bulb, or 100 joules per second.

• The storage capacity of one AA alkaline (nonrechargeable) battery is usually rated (brand new) at about 2.5 watt-hours of power. That is the same as about 9,000 watt-seconds, or 9,000 joules.

• One standard horsepower exerted for one second is 746 joules. Modern tests show that is actually a little more than the average horse can maintain. A person can maintain a sustained effort of about one-tenth horsepower.

• The solar radiation reaching the Earth amounts to 1,366 joules per square meter per second. But the efficiency of typical solar power generators is only about 10 percent.

• The combustion energy in one liter of 87-octane gasoline is 32 million joules per liter or 44.4 million joules per kilogram (or 121.1 million joules per gallon).

“But when we poured out the water, we converted its potential energy to kinetic energy, which is the form of energy of a moving object.

“Using kilograms (m for mass) and meters per second (v for velocity) produces joules.” Write this equation on the blackboard:

JOULES = (1/2)mv²

“So let’s look at our beaker of water example again. Pouring it from a height of 30 centimeters happens to produce a velocity of 2.42611 meters per second. (The formula to derive the velocity of an object after it has fallen a certain distance is the square root of twice the acceleration of gravity times the distance fallen.) Again, the mass was 340 grams.”

Distribute an appropriate number of copies of the Energy Comparisons Worksheet (S-8-7-2_Energy Comparisons Worksheet and KEY.doc).

After reviewing the students’ work and going over the answers, make these points:

• The battery power sources are shown for comparison. They cannot release all their energy quickly short of exploding.

• You’ll note that gasoline offers 68 times more energy per gram than lithium ion batteries, and 244 times more than car batteries. This may help explain why electric cars have been slow to catch on, and why researchers are constantly seeking batteries with more energy density.

The lithium ion and car batteries are rechargeable, unlike gasoline, which is combustible.

Extension:

• Assume you have built a reservoir on a hill 100 meters above a river. It is exactly the size of a football field (6,232 square meters) and is ten meters deep. Given that a cubic meter of water weighs about 1,000 kilograms (one metric ton, or tonne), what is the potential energy of the contents of the reservoir, if the water is piped down to a generator turbine at the banks of the river? (61.136 billion joules)

• Assume you can sell your resulting power for the national average of 12 cents per kilowatt hour. (A joule is the same as a watt-second.) Assuming 100 percent efficiency, what would be your revenue? ($2,037,864.00)