Part 1
Preface this section by explaining to students that the modeled solutions are simply one way to simplify the expressions. Encourage students to find and discuss other pathways to solving the problem.
“Recall the procedure for multiplying the following fractions: 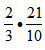 and take a moment to perform this task on your own paper.” [IS.4 - Struggling Learners]
and take a moment to perform this task on your own paper.” [IS.4 - Struggling Learners]
Give students time to recall and perform the required task. Then discuss their findings.
Possible methods:
Multiply numerators; then denominators; then simplify: 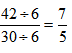
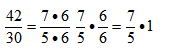
OR simplify before multiplying: 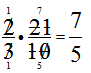
“During this lesson we will be working with problems similar to the one shown here, but instead of working with rational numbers, we will be working with rational expressions. While a rational number is the ratio of two integers, [IS.5 - Struggling Learners] a rational expression is the ratio of two polynomials and would look similar to something like this: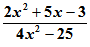 .
.
This lesson will take us through the skills required to multiply, divide, add, and subtract rational functions, which will be very similar to when we multiply, divide, add, and subtract rational numbers.”
“We will begin our lesson with multiplication.”
Model the following problems for students. Have students reflect on the type of factoring they would need to use for each part of the problem before beginning the steps.
“The rules for multiplying rational expressions require us to first make sure the numerators and denominators of the expressions are in factored form. Once they are in factored form, we should look for any common factors.” [IS.6 - Struggling Learners]
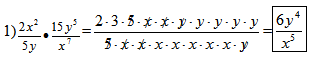
Note: This example can be done using the rules of exponents and simplifying fractions as well; the above work shows the common factors of the numerator and denominator.
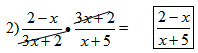
Make sure to note to students that they cannot divide by the x-terms in this situation because the x-terms are not a factor in this answer; they are being added or subtracted. Suggest substituting a trial value for the x-term to make sure the calculation is correct.
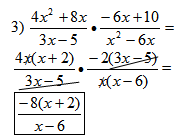
Note: This example uses the greatest common factor type of polynomial factoring.
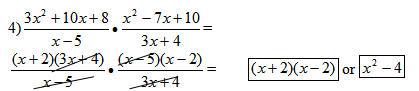
This example introduces the factoring of trinomials.
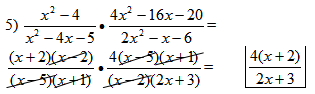
This example includes factoring of trinomials and difference of squares.
Cooperative Learning Activity: Use the following group activity to allow students to revisit and rethink through the steps of the problems. While working in groups, students will have the opportunity to work through the problems with their peers to reach the solutions to each problem. By the conclusion of the activity, students should have gained the skills necessary to perform these tasks independently.
Divide your classroom into six stations.
At each station have a problem printed out that displays the problem to be solved for the students (M-A2-5-1_Multiplying Rationals Stations Problem Set.doc).
Hand each student a Stations Activity Records Sheet (M-A2-5-1_Stations Activity Records Sheet.doc).
Divide students into groups at each station. Divide them in the manner that works best for your classroom dynamics.
Have students work at their station for an allotted amount of time (3–7 minutes). While working, monitor students’ progress and assist where necessary. Adjust timing as needed.
See M-A2-5-1_Multiplying Rationals Stations Problem Set.doc (p.7) in the Resources folder for solutions.
Part 2
Preface this section by explaining to students that the modeled solutions are simply one way to simplify the expressions. Encourage students to find and discuss other pathways to solving the problem.
“Recall the process for dividing the following fractions: 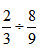 . We know there is a rule to follow when dividing fractions. However, let’s look at the reasoning behind the rule, before we state it here. The meaning of the statement is how many eight-ninths are in two-thirds? Since the reciprocal of eight-ninths is nine-eighths, because division is multiplication by the reciprocal. It is equivalent to two-thirds times nine-eighths:
. We know there is a rule to follow when dividing fractions. However, let’s look at the reasoning behind the rule, before we state it here. The meaning of the statement is how many eight-ninths are in two-thirds? Since the reciprocal of eight-ninths is nine-eighths, because division is multiplication by the reciprocal. It is equivalent to two-thirds times nine-eighths: 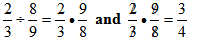
[IS.7 - Struggling Learners]
Take time to complete this problem and discuss with the class two possible methods for reaching a solution. Once they use the reciprocal of the second fraction, the students should find the methods to be similar to what they did with multiplication of fractions. Solution: (3/4)
Model the following examples for students. Make sure to point out the relationship between the work they did for the multiplying section because once the reciprocal substitution is done, the problems become identical to what they did before.
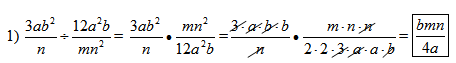
Note: This problem can be done using rules of exponents and simplifying fractions as well; the above work shows the common factors of the numerator and denominator.
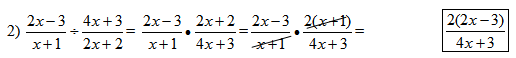
This problem involves the process of simplifying after factoring a greatest common factor and reminds students about factoring binomials.
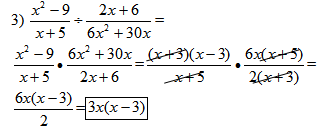
This example is designed to practice using different factoring techniques: Greatest Common Factor, difference of squares, and integers.
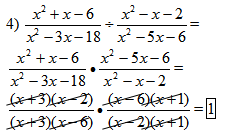
This example exposes students to trinomial factoring and what happens when everything divides by a common factor.
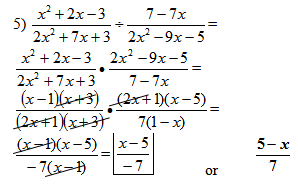
Make it clear to students how it is possible to go from 1 − x to x − 1 by factoring out −1. This example is designed to show more advanced types of complex factoring.
Learning Activity: Level Up! This activity is designed to help students get to the point of completing the most advanced type of division problems independently. Students will begin with a simple problem, and as they work through the steps of the activity they will try to reach the ultimate goal of completing an advanced problem. This will help to address the needs of those students who need opportunities for additional learning while allowing students at or beyond the standards the opportunity to move forward.
Instructions: Prior to the activity, cut out the problems from the Level Up! Problem Set into strips (M-A2-5-1_Level Up Problem Set and KEY.doc).
To begin the activity, pass out problem 1 to each student (most basic problem). Students are to work on the problem independently while the teacher addresses students’ needs where appropriate. Once a student has satisfactorily completed the problem, he/she receives a problem one level harder and repeats the process. The teacher may consider adding a rewards system for each level that is passed to help motivate students. Solutions to this activity can be found on page three of the Level Up! Problem Set document (M-A2-5-1_Level Up Problem Set and KEY.doc).
Part 3
Preface this section by explaining to students that the modeled solutions are simply one way to simplify the expressions. Encourage students to find and discuss other pathways to solving the problem.
“When adding and subtracting fractions, what is the rule that we have to follow?” Students should answer that a common denominator is needed. [IS.8 - Struggling Learners]
“Looking at the following sum,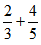 , what would the common denominator be ?” (15)
, what would the common denominator be ?” (15)
“What do we have to do to make these two fractions have a common denominator?” Multiply the numerator and denominator of the first fraction by 5 and then multiply the numerator and denominator of the second fraction by 3, thereby creating the new equivalent sum: 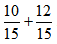 . Ask students whether they can think of another way to derive equivalent fractions with the same denominator.
. Ask students whether they can think of another way to derive equivalent fractions with the same denominator.
“Once we have a common denominator we can add these two fractions, but make sure when you add or subtract that you are only doing so with the numerators; the denominator stays as it is. Therefore, the sum is (22/15).”
“The same rules that are necessary when adding or subtracting numbers are also required when adding or subtracting rational expressions. In other words, we must have common denominators. We multiply by (5/5) which is really multiplying by 1.”
“To begin a problem involving the adding or subtracting of rational expressions, the first thing we have to do is make sure the denominators are in factored form. This will allow us to find a common denominator more easily.”
Prior to modeling the examples of how to add and subtract rational expressions, use the Common Denominator Practice Sheet to help students get used to the process of determining the LCM of the two denominators so they can perform this task more efficiently when completing the addition and subtraction problems (M-A2-5-1_Common Denominators and KEY.doc).
Model the following examples for students, carefully guiding them through the process of finding the common denominator and then the process required to combine the two fractions.
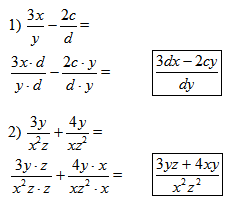
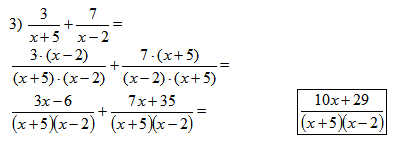
When discussing this example with students, make sure to emphasize the important steps involved (factoring, distributing, and combining like terms).
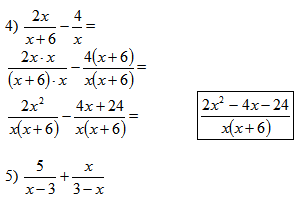
Use this example as an opportunity to discuss the relationship between the two denominators and how factoring out −1 will help reach the LCD.
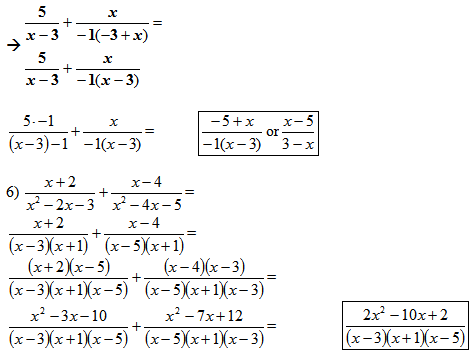
Note that this example begins with factoring. Make sure to emphasize that this must be done before finding a common denominator. Be sure to remind students about multiplying the numerators before combining like terms.
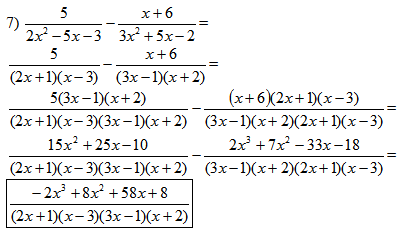
This example is more advanced with the level of factoring, multiplying, and combining like terms.
Part 4
Introduce students to the idea of a rational function, i.e., a function given by a rational expression. A rational number is one that can be expressed as the ratio (or the quotient) of two integers.
Solve the following problem:
Billy’s Boat Repair Shop manager wants to determine his profit for last month. He has concluded that the revenue can be modeled by the function 
and the costs can be modeled by the function 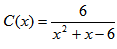 ,
,
where x is the number of engines repaired.
Find a function P(x) that can model profit for Billy’s Boat Repair Shop. Determine the profit for repairing 12 boats.
[Solution: P(x) = 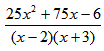 ; $29.96]
; $29.96]
· As an Exit Ticket: have students write a brief statement responding to the following: How are multiplying and dividing rational expressions the same/different?
· After going through topic 1, use the independent practice worksheet (M-A2-5-1_Multiplying Rationals IP and KEY.doc) to provide students with extra practice. The problems range from basic to most advanced. If necessary, assign specific problems to students based on their needs. Solutions can be found on page 2 of the document.
· Use guided notes packets provided in the Resources folder for students who need opportunity for additional learning (M-A2-5-1_Operations Guided Notes.doc).
Extension:
· Use the Level Up! Problem Set (M-A2-5-1_Level Up Problem Set and KEY.doc) as a homework assignment if it is not possible to complete in class. Adjust required problems to be done by students depending on their levels, if necessary.
· Division Application Extension: If the area of a rectangle is and the width is , what is the length? Solution: (3x + 7)
· After going through topic 3, use the independent practice worksheet (M-A2-5-1_Adding Subtracting IP and KEY.doc; solutions on page 2 of document) to provide students with extra practice. The problems range from basic to most advanced. If necessary, assign specific problems to students based on their needs.
