Building a Foundation for Multiplication
Building a Foundation for Multiplication
Objectives
This unit uses hands-on activities and word problems to help students develop strategies for learning basic multiplication facts. Students are encouraged to demonstrate their thinking processes in computation, using a variety of methods and tools, including objects, pictures, number lines, and skip counting. Students will:
- use skip counting of equal groups to solve equal-groups problems.
- draw/model their thinking for solving equal-groups story problems.
Essential Questions
How are relationships represented mathematically?
How can patterns be used to describe relationships in mathematical situations?
How is mathematics used to quantify, compare, represent, and model numbers?
- How is mathematics used to quantify, compare, represent, and model numbers?
- How can patterns be used to describe relationships in mathematical situations?
Related Unit and Lesson Plans
Related Materials & Resources
The possible inclusion of commercial websites below is not an implied endorsement of their products, which are not free, and are not required for this lesson plan.
- www.nctm.org
- http://illuminations.nctm.org
- www.aaamath.com
- www.dr-mikes-math-games-for-kids.com
- Interactive-number-line addition activity: http://www.funbrain.com/linejump/index.html
- 0–20 number line: www.abcteach.com/free/n/numberline_0to20.pdf
- Amanda Bean’s Amazing Dream by Cindy Neuschwander
Formative Assessment
-
View
Short-Answer Items
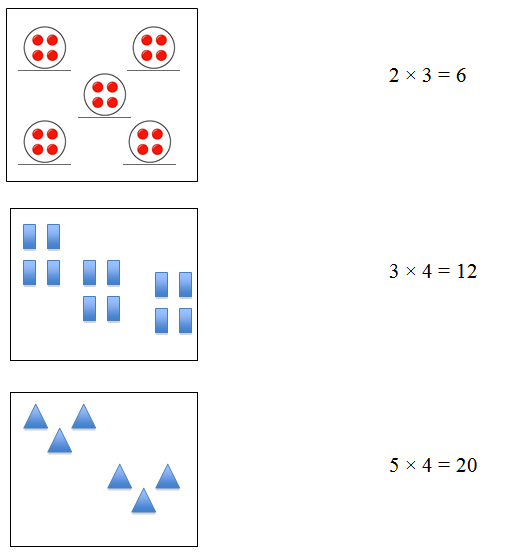
- Draw a line from each set of equal groups to the number sentence that describes it.
- Draw a representation for each number sentence (or equation).
6 × 2 = ___
4 × 4 = ___
Read the stories. Draw a representation; then write a number sentence to show how to solve it.
- 5 cars are parked in the parking lot. If each car has 4 wheels, how many wheels are there in the parking lot?
_________________________________
- 3 students have 3 pencils each. How many pencils do they have altogether?
_________________________________
Show using pictures, counters, or words and write the number sentence:
- Five groups of three
- Seven groups of two
- Four groups of four
Short-Answer Key:
- Draw a line from each set of equal groups to the number sentence that describes it.
- Draw a representation for each number sentence (or equation).
6 × 2 = 12 (representations may vary)
4 × 4 = 16 (representations may vary)
Read the stories. Draw a representation; then write a number sentence to show how to solve it.
- 5 cars are parked in the parking lot. If each car has 4 wheels, how many wheels are there in the parking lot?
5 × 4 = 20 (representations may vary)
- 3 students have 3 pencils each. How many pencils do they have altogether?
3 × 3 = 9 (representations may vary)
Show using pictures, counters, or words and write the number sentence:
- Five groups of three
5 × 3 = 15 (representations may vary)
- Seven groups of two
7 × 2 = 14 (representations may vary)
- Four groups of four
4 × 4 = 16 (representations may vary)
Performance Assessment:
Materials:
- manipulatives
- paper and pencils
- document camera or overhead projector
Procedure:
Hand out a blank piece of paper to each student.
Put the following question on an overhead or under the document camera:
Show how you solved this problem by using pictures, numerals, or words.
“Target has 4 tricycles. Each tricycle has 3 wheels. How many wheels do they have all together?”
The student should show his/her work and explain how s/he solved the problem.
Performance Assessment Key and Scoring Rubric:
Possible responses may include:
4 + 4 + 4 = 12
4 × 3 = 12
(representations may vary)
Points
Description
4
- Model of work is clear and accurate.
- Verbal explanations are thorough, detailed, and clear.
- Student displays excellent understanding of the questions, mathematical concepts, and processes.
- Student performs beyond the problem requirements and possibly demonstrates multiple methods or solutions.
- Written number sentence is accurate.
3
- Model of work is clear and accurate.
- Verbal explanations are thorough.
- Student displays appropriate understanding of the questions, mathematical concepts, and processes.
- Written number sentence is accurate.
2
- Model of work is unclear or has minor mistakes.
- Verbal explanations are present but lacking some detail.
- Student displays partial understanding of the questions, mathematical concepts, and processes.
- Written number sentence is inaccurate.
1
- Model of work is unclear and inaccurate.
- Verbal explanations are incomplete and lack detail.
- Student displays little understanding of the questions, mathematical concepts, and processes.
- Written number sentence is inaccurate.
0
- Model of work is not attempted.
- Verbal explanations are illogical or not present.
- Student displays no understanding of the questions, mathematical concepts, and processes.
- Written number sentence is missing.
- Draw a line from each set of equal groups to the number sentence that describes it.
Final 5/12/14
