During the lesson, monitor students’ understanding of the following points, and adjust their understanding as necessary, to help ensure that students can master the targeted learning goals within the time frame:

• Students’ understanding of gravity will be assessed through their responses to the gravity demonstration.
• The appropriate use and application of Kepler’s Third Law of Planetary Motion will be assessed through class discussion and by student/group monitoring throughout the activity.
• Collect the Kepler Worksheet for individual assessment.

Open the subject with the following narrative:

“It was 1666, probably in late summer. Twenty-three-year-old graduate student Isaac Newton was at his family farm about 100 miles north of London. He was home because his university had suspended classes because of the outbreak of plague in London. The epidemic would continue until a huge fire suddenly burned down much of the city. The government then went broke, and the king laid off most of the navy, despite the fact that he was at war with Holland. The Dutch would then raid the main British naval base, tow off one battleship as a souvenir, and set fire to the rest. It was, in other words, a good time to find something diverting to think about.

For Newton, the diversion was provided by an apple tree. He saw an apple do something that was, to him, at that moment, intriguing.”

Hold out the apple and let it fall to the ground.

Invite the class to describe what just happened.

There will presumably be a consensus that the apple fell to the ground.

However, explain to students that, more specifically, the apple accelerated toward the center of the Earth. Apparently, the Earth has some power of attraction over the apple.

But the Earth spreads out to the horizon. “Why did the apple go straight down?”

Newton assumed that the sum of the attraction was at the center of the Earth, and that the masses on either side of it canceled each other out. But how far out did this force extend? For instance, could it reach to the moon? If so, it probably reached out indefinitely, and was the governing factor in celestial mechanics.

There was an assumption that celestial bodies were governed by different powers than those at work on the surface of the Earth. Anyway, how could the moon be influenced by the Earth when they were so far apart? Doing so required “influence at a distance,” which ranked with ghost stories.

But if the sum of the Earth’s attraction was at the Earth’s center, then here on the Earth’s surface, about 6,400 kilometers (about 4,000 miles) from its center, we were already being influenced from a distance. Why would it not extend farther?

Newton set out to find a convincing demonstration that the force guiding the orbit of the moon was an extension of the force that we feel here on Earth.

First, he calculated how much the moon is being deflected from a straight path through space. His calculations showed that the moon experienced a deflection toward the Earth—if that’s what it was—of about 13 feet per minute. We don’t know exactly how he derived this figure.

He was aware of Kepler’s calculations concerning the motions of planets, which showed that their orbital motions reduced speed as they became farther from the sun. In fact, the results implied that the attraction of the sun fell off according to the square of the distance. In other words, something that was twice as far away experienced a quarter of the force, etc.

If the moon was under the control of the Earth’s attraction, then the attraction that the moon experienced should follow the same “inverse square” ratio. Now let’s review Newton’s Law of Universal Gravitational, which utilized the principles of the Inverse Square Law.

The Gravitational force between Earth and the moon is attractive and the force exerted on moon by Earth (F₁) is equal in magnitude to the force exerted on the Earth by the moon (F₂). See diagram below.

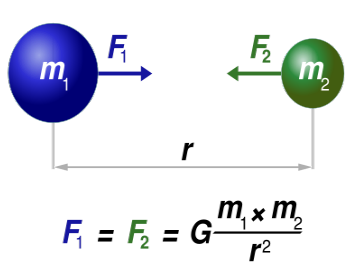
Gravitational force depends on the distance between the two masses involved. If the mass of two objects (m₁ and m₂) are separated by a distance (r), the magnitude of the gravitational force is given by the equation above.

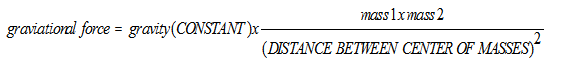
To establish whether this was so, he needed three pieces of information.

Write these numbers on the board:

• 6,371 kilometers (the distance to the center of the Earth)
• 400,000 kilometers (approximate distance to the moon)
• 9.8 meters/second squared (force of gravity at the Earth’s surface)

Ask for a volunteer to use a calculator or to populate a spreadsheet during this demonstration.

Continue the discussion by explaining that Newton presumably made these three calculations:

1. First, he found the ratio between the attraction at the surface of the Earth and at the moon’s distance. If the attraction truly falls off by the square of the distance, the ratio would be the distance to the moon squared, divided by the distance from the center of the Earth to the surface, squared. (The answer should be 3,941.89.)

2. Next he discovered how far something would fall in a minute on the Earth’s surface. Since the acceleration of gravity here on the surface is 9.8 meters per second square, we square 60 and multiply it by 9.8. Then, since we started accelerating from zero, we divide the total in half. (The answer should be 17,640 meters. Since this is more than 1,050 kilometers per hour, or more than 650 miles per hour, caution students that in the atmosphere an object would reach terminal velocity before reaching such speeds.)

3. Finally, he divided the one-minute fall on the surface in Step 2 by the ratio found in Step 1. The result is 4.48 meters, or 14.68 feet.

That’s very close to the 13 feet Newton had calculated for the moon’s deflection, based on approximate values. Newton performed the calculations more than once over a period of years using different values. He became convinced that what we feel here on the Earth is the same force that the moon is experiencing.

But what about the rest of the solar system? If the Earth’s gravity controls the orbit of the moon, it seems logical to infer that the gravity of the sun controls the orbits of the planets. But that seemed to be asking a lot as the distances involved are huge. In fact, at the time they had only a vague idea what those distances were.

At this point, define the Astronomical Unit (AU), a unit of measurement that equals the distance between the Earth and the sun. While Newton and his colleagues did not know how far away the planets were, they could track precisely how the planets appeared to change location as the Earth moved around the sun in its orbit. This let them plot triangles, the base of which was the distance between the Earth and sun. The other two sides were the distance from the planet to the Earth, and from the planet to the sun.

When you know the angles of the corners of a triangle, and the length of one side, you can use trigonometry to find the length of the other two sides. In this case they did not know the length of any of the three sides, but they knew that one side, stretching between the Earth and the sun, remains about the same. So they called that side AU, and figured the other sides in proportion to AU.

During Newton’s lifetime, astronomers realized that previously accepted values for AU were too low by a factor of about 20. Considerable work by leading astronomers went into refining the value of AU, and a value close to the currently accepted distance was reached by 1659. However, total accuracy and laser light (and direct measurement) had to wait for the invention of radar.

But as it turns out, knowing orbital distances for the planets in AUs, and orbital periods in years, is enough to show that the sun’s gravity extends into the farthest reaches of the solar system. Orbital periods for the planets had long been established. As early as 1605 (before astronomical telescopes were invented) mathematician Johannes Kepler (1571–1630) established that the orbital period of a planet had a direct relationship to its distance from the sun. Not only did orbital speeds get slower for bodies farther from the sun, but he found a constant relationship:

• The cube of the planet’s distance from the sun was directly proportional to the square of the orbital period.

Using D to stand in for the planet’s distance from the sun, and P to stand in for its orbital period, the formula for the relationship, now called Kepler’s Third Law of Planetary Motion, looks like this (write on the board):

• D³ = P²

Distribute copies of the Kepler worksheet (S-8-1-3_Kepler Worksheet.doc). Depending on the availability of equipment, students can work on it individually, each with a calculator or PC, or gather in groups, each having a calculator or PC with one person running it. But to drive home the lesson, each student should complete a worksheet. If there is only one calculator or PC in the class, have a volunteer use it to perform the operation and write the result on the board, which students can copy.

Restate the instructions on the worksheet: cube D for each body and then take the square root of the resulting number and enter it into the Calculated Orbital Period column. The value for Earth is already entered. (It’s trivial: 1 cubed is one, and the square root of 1 is 1.)

The results, rounded to two decimal places and shown in italics, should look like this:

When all calculations are completed, assess student outcomes After each value is given, ask for feedback on how close it is to the calculated value.

The observed orbital periods are as follows:

Continue the lesson by making two points:

• The calculated results were almost indistinguishable from the observed results.
• Ceres, Uranus, Neptune, Pluto, and Eris were not known to exist in Kepler’s time, yet his Third Law fits their orbits, too.

We can confidently state that Kepler’s relationship is the result of underlying physical laws and not a numerical coincidence. It implies that the influences of the sun extend into the farthest regions of space. Today it is accepted that its influence extends into interstellar space until it is canceled out by the influence of other stars.

Because of gravity, the moon orbits the Earth, and the Earth and other planets orbit the sun. The sun, meanwhile, orbits the center of the galaxy.

Extension:

• Students can divide the observed orbital value by the calculated value for each body on the worksheet. All the values should round to 1, but some calculated values will be a better fit than others.
• Lead a discussion of why the fit is not perfect. The reasons include:
• The planets disturb each other’s orbits with their gravity as they move.
• The orbits of the planets are ellipses rather than circles, so Kepler’s relationship is a simplified model of what is happening in the solar system.