• In the Lesson 3 Exit Ticket, students have to make a qualitative assessment of their understanding of the relationship between the polynomial expression and its functional representation as a graph. The activity requires them to indicate and identify the significant elements of a polynomial function including its shape, roots, minimum, and maximum. [IS.13 - Struggling Learners]

Start this lesson with a discussion about being sick and taking medicine. Generally, when medication enters a body, its presence diminishes over time. Any medication’s rate of decrease varies with the type of medication, its dosage, and the physical condition of the patient. Ask the following questions:

• “How many of you have been sick before?”

• “How many of you have taken medication to make you feel better?”

• “How does medicine work?”

Activity 1: [IS.7 - Struggling Learners] Graphing Elapsed Time “With your partners, discuss what the graph would look like if you were to graph the amount of medicine in the bloodstream (y-axis) versus time (x-axis).” Give students about five minutes; then, have them create groups of four to share their thoughts. Encourage them to sketch graphs. “Is the graph a line? A parabola? A cubic or quartic?" [IS.8 - Struggling Learners]  After another five minutes, have a class discussion and see what students are thinking. Don’t reveal the graph yet, but let students know that today’s lesson is going to illustrate properties of polynomial graphs and how polynomial functions are used to model different real-world situations.

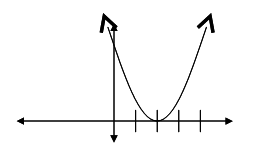
“What does the degree of a polynomial tell us about its graph?” Students may say that the degree tells us how many roots or x-intercepts the graph has. You can then draw a graph of a parabola with a vertex at (2, 0), as shown, and ask the following questions:

• “What degree polynomial is illustrated by the graph of a parabola?”

• “How many x-intercepts should it have?”

• “Why doesn’t this graph have two x-intercepts?”

• “Take a look at the equation of the parabola by inserting the vertex into the graphing form of a parabola and write it in factored form and standard form:

• y = (x − 2)²

• y = (x − 2)(x − 2)

• y = x² − 4x + 4”“In the previous lesson, what did we learn about factors and roots?”

(If x − 2 is the factor, then 2 is the root; in this case, 2 is both roots.)

Put the following on the board for students to copy into their notes.

Example: y = (x − 2)²

y = (x − 2)(x − 2)

y = x² − 4x + 4

Multiplicity: This example illustrates multiplicity of roots. Since x − 2 occurs twice as a factor, 2 is called a double root.

• When a root has an even multiplicity, the graph “bounces off” the x-axis (as in the above example).

• When a root has an odd multiplicity, the graph crosses the x-axis.

• When listing the roots of a polynomial, state the multiplicity of the roots.

• Example: The roots of y = x³ − 6x² + 12x − 8 are 2, 2, and 2 (triple root).

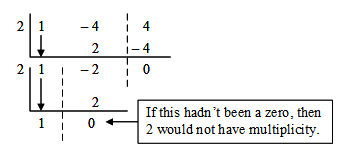
• If synthetic division is used to prove a number has multiplicity as a root, you can do the synthetic division as many times as its multiplicity.

Example: Using the parabola that represents y = x² − 4x + 4 from above.

Activity 2: Working on Polynomial Roots in Pairs

“In your pairs, one of you is A and the other is B.” Give Student A questions (a) and (c). Give Student B questions (b) and (d).

a) x³ −3x² −9x − 5, roots − 1 and 5 (− 1 is a double root)

b) x⁴ − 12x³ + 48x² − 64x, roots 0 and 4 (4 is a triple root)

c) x⁴ + 2x³ − 11x² − 12x + 36, roots − 3 and 2 (− 3 and 2 are both double roots)

d) x⁵ − 2x⁴ + x³, roots 0 and 1 (0 is a triple root and 1 is a double root)

Students should notice that the number of roots given does not equal the degree of the polynomial. “Your task is to determine which root has multiplicity or if both roots do. Student A is going to read a polynomial to Student B and provide the given roots. Student B must use synthetic division to prove which root has multiplicity or if both do. When B is done, A will check B’s work and then you will switch roles. Each of you will read two polynomials to your partner.”

“The number of roots is not the only thing determined by a polynomial’s degree. Take a look at the parabolas on the board (vertex at 0, 0).”

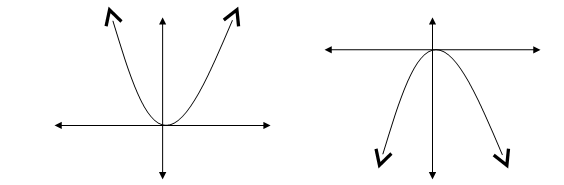
“Do you know the equations of these two parabolas?”

(The first graph is y = x² and the second graph is y = −x².)

“What changed from the first graph to the second?”

“What changed from the first equation to the second?”

“Now take a look at the graphs of two cubic equations.”

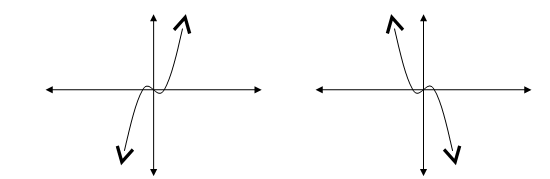
“The first graph is y = x³ and the second graph is y = −x³. What are one similarity and one difference between the cubic graphs and the parabolas?” Be sure someone mentions the fact that the negative symbol reflects (flips) the graph over the x-axis. Also make sure there is conversation about the “end behavior” of the graphs (i.e., the parabola’s ends go in the same direction and the cubic graph’s ends go in opposite directions).

Below is a table that students could add to their notes. “Recall that the leading coefficient is the number in front of the variable with the largest degree. For example, in the polynomial 6x⁵ + 2x⁴ − x³ +3x² + 4x − 7 the leading coefficient is 6.”

“The sign of the lead coefficient determines the right end behavior, and the degree determines the left end behavior.”

[IS.9 - Struggling Learners]

	Positive Leading Coefficient	Negative Leading Coefficient
Even Degree
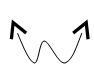
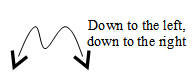
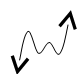
Odd Degree	Down to the left, up to the right	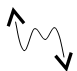Up to the left, down to the right

“Since polynomial graphs don’t have an ‘end point,’ there isn’t a unique minimum or maximum, so polynomials are often described with ‘local minima’ or ‘local maxima.’ These points illustrate where the graph changes direction.”

Put these definitions on the board for students to add to their notes.

Local Minima: points where the graph changes from decreasing to increasing.

Local Maxima: points where the graph changes from increasing to decreasing.

Activity 3: Plotting Minima and Maxima

Put the following table on the board and have students come up one or two at a time to fill it in. [IS.10 - Struggling Learners][IS.11 - All Students]   Have them do this silently. Erase any incorrect answers, but do not explain what they did wrong, so they will try to figure it out on their own. Tell them to ignore the last two columns for now.

Have students sketch graphs individually of the polynomials that have local minima and maxima in the table. They should first plot the minima and maxima, then look at the end behavior, and then sketch the graph. When they are done, have them compare their work to another student’s. They should discuss if there are any differences between their graphs.

The last part of this lesson ties in this new information with the opening activity. Put four different graphs on the board: one linear, one quadratic, one cubic, and one quartic. Ask students if for the opening medication problem any of them drew a shape similar to one of these four. Go over each graph in the medication context and see which one makes the most sense to them now.

Activity 4: Determining End Behavior

Put the following problem on the board for students to read:

“Suppose a person takes an aspirin and five hours later takes another one. The amount of medication in the bloodstream can be represented by the polynomial equation
y = − .0108x⁴ + .316x³ − 3.0231x² + 10.8668x − 5.3507 where x is the time elapsed since taking the medication and y is the amount of medication in the bloodstream in tenths of a percent.”

“What is the end behavior for this polynomial? Graph the equation using a calculator and answer the following questions:”

• “For which values of x does the graph make sense? Why?”
  [0.581 ≤ x ≤ 14.78; values of x for which range is positive]

• “How much medicine is in the bloodstream after 1 hour? After 13 hours?”
  [2.798 units; 10.8 units]

• “When is the medicine at its maximum potency?”
  [approximately 12 hr.]

• “What does the local minimum mean in terms of the amount of medicine in the bloodstream and when the person takes the second aspirin?”
  [local maximum at 3 hr.; maximum at 12 hr.]

Activity 5: Graph Sketching in Pairs or Small Groups [IS.12 - All Students]

“In pairs, you are to sketch graphs of polynomials with the given key points. When you are done, pair up with another pair to discuss the graphs. When everyone is done, I will call on individuals to come to the front of the class to show an answer to one of the problems.”

1. Roots at − 4, − 1 and 3 with a local maximum at (− 3, 3) and local minimum at (1, − 3)

2. Roots at −1 (double) and 1 (double) with a local maximum at (0, 1) and local minima at (−1, 0) and (1, 0)

3. Roots at −5, −3, −1, 1 and 3 with local maxima at (−2, 4) and (2, 2) and local minima at (−4, −1) and (0, −2)

Use the Lesson 3 Exit Ticket (M-A2-3-3_Lesson 3 Exit Ticket.doc and M-A2-3-3_Lesson 3 Exit Ticket KEY.doc) to evaluate students’ understanding.

Extension:

• Sketch the graph and find the roots and locations of local minimum and maximum for the polynomial function x³ – 9x² + 20x. Indicate whether the points are minimum or maximum. [roots: 0, 4, 5; local minimum between (4, 0) and (5, 0); local maximum between (1, 12) and (2, 12)]