Line of Best Fit
Line of Best Fit
Objectives
In this unit, students understand how variables relate to one another. Students will:
- categorize scatter plots by their correlation.
- create scatter plots.
- draw lines of best fit and write the equations of lines of best fit.
- make predictions using the line of best fit.
Essential Questions
- How can we determine if two variables correlate linearly?
- How can we use data to make predictions about the future?
Related Unit and Lesson Plans
Related Materials & Resources
The possible inclusion of commercial websites below is not an implied endorsement of their products, which are not free, and are not required for this lesson plan.
- https://www.purplemath.com/modules/scattreg2.htm
- http://dictionary.reference.com/browse/correlation (for definition of correlation)
- http://faculty.washington.edu/chudler/words.html
- http://illuminations.nctm.org/ActivityDetail.aspx?ID=146
- http://mathbits.com/mathbits/tisection/statistics1/linefit.htm
- http://illuminations.nctm.org/LessonDetail.aspx?id=L254 (This lesson is based off the illuminations lesson.)
- http://illuminations.nctm.org/LessonDetail.aspx?id=L298 (Exit Ticket is from this illuminations lesson.)
Formative Assessment
-
View
Multiple-Choice Items
1. What type of correlation does the following graph have?
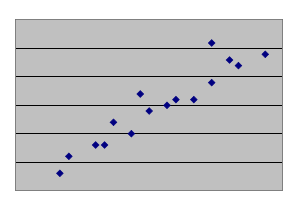
A
positive linear correlation
B
negative linear correlation
C
no correlation
D
nonlinear correlation
2. Which of the following does not have negative correlation?
A
number of hours watching TV per week versus grade-point average
B
car weight versus miles per gallon
C
height versus weight
D
price of an item versus number of people who want it
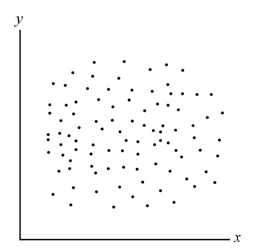
3. The scatter plot has what type of correlation?
A
nonlinear correlation
B
no correlation
C
negative linear correlation
D
positive linear correlation
4. The equation for the line of best fit is written in what form?
A
slope-intercept form
B
standard form
C
point-slope form
D
vertex form
5. In the Stroop Lab, what does the slope represent?
A
number of words in the list
B
color of the word
C
number of correct matches
D
seconds per word
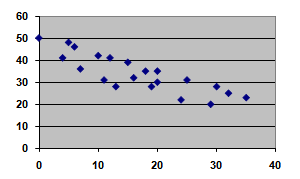
6. Which equation best represents the line of best fit for the following scatter plot?
A
y = x + 50
B
y = −50x + 1
C
y = −x + 50
D
y = x – 50
7. Equations of lines of best fit are used for what?
A
to tell stories
B
to make predictions
C
to draw graphs
D
to prove correlation
8. The line of best fit for time versus the cost of a gallon of milk is y = .02x + .10 where x represents the number of years after 1930 and y represents cost. What was the cost of a gallon of milk in 1970?
A
$0.90
B
$39.50
C
$1.50
D
$4.80
9. The line of best fit for time versus the cost of a gallon of milk is y = .02x + .10 where x represents the number of years after 1930 and y represents cost. In what year was milk $1.20 per gallon?
A
1940
B
1955
C
1985
D
1995
Multiple-Choice Answer Key
1. A
2. C
3. B
4. A
5. D
6. C
7. B
8. A
9. C
Short-Answer Items:
10. Graph a scatter plot that has a negative correlation.
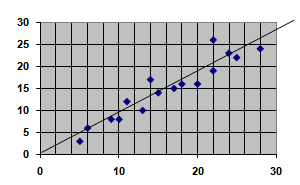
11. The line of best fit is drawn in the scatter plot. What is the equation of the line of best fit?
12. Plot the following data, draw a line of best fit, and write the equation of the line of best fit.
x
0
1
2
3
4
5
6
7
10
y
2
5
9
10
14
19
21
25
30
Short-Answer Key and Scoring Rubrics:
10. Graph a scatter plot that has a negative correlation.
Answers will vary.
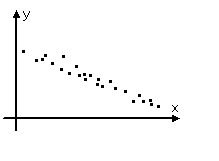
11. The line of best fit is drawn in the scatter plot. What is the equation of the line of best fit?
y = (7/6)x
12. Plot the following data, draw a line of best fit, and write the equation of the line of best fit.
x
0
1
2
3
4
5
6
7
10
y
2
5
9
10
14
19
21
25
30
y = 2.954x + 2.528 (from calc)
Points
Description
3
· An accurate line of best fit has been drawn on a scatter plot with axes labeled.
· An accurate equation for the line of best fit has been provided.
2
· The scatter plot is made and there is a line of best fit but no equation.
1
· The line of best fit equation is provided, but there is no scatter plot or line of best fit drawn.
0
· The student’s response is incorrect, irrelevant, too brief to evaluate, or missing.
Performance Assessment:
Research and find two variables that have linear correlation.
1. Make a table of values with your data.
2. Make a scatter plot of your data and label the axes.
3. Draw in a line of best fit.
4. Write the equation of the line of best fit:
5. What does the slope represent in terms of your data?
6. What does the y-intercept represent in terms of your data?
7. Using your line of best fit, write one question in which you have to solve for y. Show the answer.
8. Using your line of best fit, write one question in which you have to solve for x. Show the answer.
Performance Assessment Scoring Rubric:
Points
Description
5
The student has the following:
· a table with data that correlates linearly
· a scatter plot with axes labeled
· a graph of the line of best fit
· the equation of the line of best fit
· a proper explanation of the slope
· a proper explanation of the y-intercept
· one question and answer in which solving for y
· one question and answer in which solving for x
4
The student has the following:
· a table with data that correlates linearly
· a scatter plot, but axes are not labeled
· a graph of the line of best fit
· the equation of the line of best fit
· a proper explanation of the slope
· a proper explanation of the y-intercept
· one question and answer in which solving for y
· one question and answer in which solving for x
3
The student has the following:
· a table with data that correlates linearly
· a scatter plot, but axes are not labeled
· the equation of the line of best fit, but not its graph
· a proper explanation of the slope
· a proper explanation of the y-intercept
· one question and answer in which solving for y
· one question and answer in which solving for x
2
The student has the following:
· a table with data that correlates linearly
· the equation of the line of best fit
· incorrect explanations of slope and y-intercept
· one question and answer in which solving for y
· one question and answer in which solving for x
1
The student has the following:
· a table with data that correlates linearly
· the equation of the line of best fit
· incorrect explanations of slope and y-intercept
· one question but missing the answer in which solving for y
· one question but missing the answer in which solving for x
0
The student’s response is incorrect, irrelevant, too brief to evaluate, or missing.
DRAFT 11/03/2010
